题目内容
【题目】如图①,水平桌面上有甲、乙、丙三个圆柱形容器,它们的高都为![]() 且甲、丙容器的底面积相同,乙容器在距离底部
且甲、丙容器的底面积相同,乙容器在距离底部![]() 高度处与甲、丙容器连通(联通处的体积忽略不计).甲容器中有水,水位高为
高度处与甲、丙容器连通(联通处的体积忽略不计).甲容器中有水,水位高为![]() .若用水管向乙容器中匀速注水,直至三个容器都注满水,乙容器中的水位
.若用水管向乙容器中匀速注水,直至三个容器都注满水,乙容器中的水位![]() 与注水时间
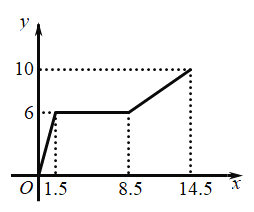
与注水时间![]() 之间的函数图象如图②所示.
之间的函数图象如图②所示.
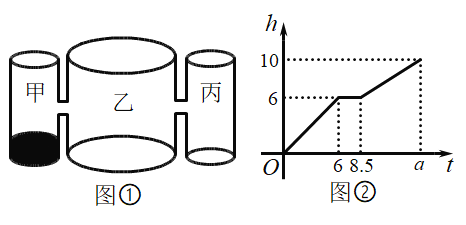
(1)甲、乙两容器的底面积之比为 ;
(2)图②中![]() 的值为 ;
的值为 ;
(3)若将注水管改为向容器丙中匀速注水,且注水速度不变,请在图③中画出容器丙中水位![]() 与注水时间
与注水时间![]() 之间的函数图象.
之间的函数图象.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)如图所示见解析.
;(3)如图所示见解析.
【解析】
(1)观察图象即可知:单独加水到乙容器6cm处要6分钟,然后再将甲丙加水到题意高度用了2.5分钟,由匀速注水列方程即可解决问题;
(2)根据容器总体积除以每分钟加水体积即可解答;
(3)根据题意先加水丙到6cm,再加加到6cm,再加甲到6cm处,最后一同加满,由此计算即可画出图像.
解:(1)设甲容器底面积为s,甲乙容器的底面积之比为k,依题意得:
![]() ,解得:
,解得:![]() ,
,
故答案为:![]() ;
;
(2)设甲容器底面积为s,所以需加水体积为:![]() ,
,
加水速度为![]() ,
,
∴加水总时间为:![]() (秒)
(秒)
故答案为:![]() ;
;
(3)如图所示:
0
由(2)可知丙容器加至6cm处所需时间为:![]() (秒),
(秒),
甲乙容器加至6cm处所需时间为:![]() (秒),此时丙容器高度不变,即到8.5秒时高度为6cm不变,
(秒),此时丙容器高度不变,即到8.5秒时高度为6cm不变,
最后加满容器由(2)可知加水总时间为![]() 秒.
秒.
故图象如图所示.

 阅读快车系列答案
阅读快车系列答案【题目】某小区超市一段时间每天订购80个面包进行销售,每售出1个面包获利润0.5元,未售出的每个亏损0.3元.(1)若今后每天售出的面包个数用x(0<x≤80)表示,每天销售面包的利润用y(元)表示,写出y与x的函数关系式;
(2)小明连续m天对该超市的面包销量进行统计,并制成了频数分别直方图(每个组距包含左边的数,但不包含右边的数)和扇形统计图,如图1、图2所示,请结合两图提供的信息,解答下列问题:
①m的值为 ;
②求在m天内日销售利润少于32元的天数;
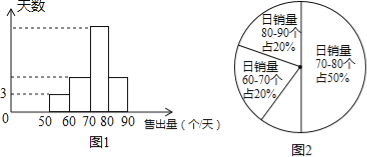
(3)如图(2)中m天内日销售面包个数在70≤x<80这个组内的销售情况如表:
销售量/个 | 70 | 72 | 73 | 75 | 78 | 79 |
天数 | 1 | 2 | 3 | 4 | 3 | 2 |
请计算该组内平均每天销售面包的个数.