题目内容
【题目】广元市某中学举行了“禁毒知识竞赛”,王老师将九年级(1)班学生成绩划分为A、B、C、D、E五个等级,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题:
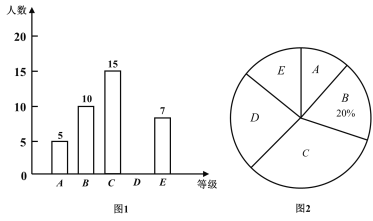
(1)求九年级(1)班共有多少名同学?
(2)补全条形统计图,并计算扇形统计图中的“C”所对应的圆心角度数;
(3)成绩为A类的5名同学中,有2名男生和3名女生;王老师想从这5名同学中任选2名同学进行交流,请用列表法或画树状图的方法求选取的2名同学都是女生的概率.
【答案】(1)50;(2)见解析,108°;(3)![]() .
.
【解析】
(1)由B的人数和其所占的百分比即可求出总人数;
(2)C的人数可知,而总人数已求出,进而可求出其所对应扇形的圆心角的度数;根据求出的数据即可补全条形统计图;
(3)列表得出所有等可能的情况数,找出刚好抽到2名同学都是女生的情况数,即可求出所求的概率.
解:(1)由题意可知总人数=10÷20%=50名;
(2)补全条形统计图如图所示:
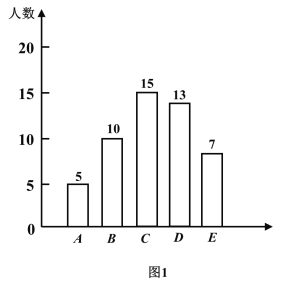
扇形统计图中C等级所对应扇形的圆心角=15÷50×100%×360°=108°;
(3)列表如下:
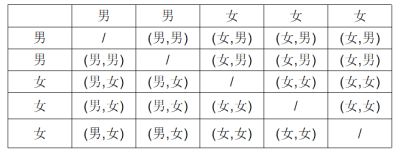
得到所有等可能的情况有20种,其中恰好抽中2名同学都是女生的情况有6种,
所以恰好选到2名同学都是女生的概率=![]() =
=![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某公司计划投入50万元,开发并生产甲乙两种产品,根据市场调查预计甲产品的年获利y1(万元)与投入资金x(万元)成正比例,乙产品的年获利y2(万元)与投入资金x(万元)的平方成正比例,设该公司投入乙产品x(万元),两种产品的年总获利为y万元(x≥0),得到了表中的数据.
x(万元) | 20 | 30 |
y(万元) | 10 | 13 |
(1)求y与x的函数关系式;
(2)该公司至少可获得多少利润?请你利用所学的数学知识对该公司投入资金的分配提出合理化建
议,使他能获得最大利润,并求出最大利润是多少?
(3)若从年总利润扣除投入乙产品资金的a倍(a≤1)后,剩余利润随x增大而减小,求a的取值
范围.