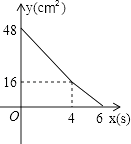
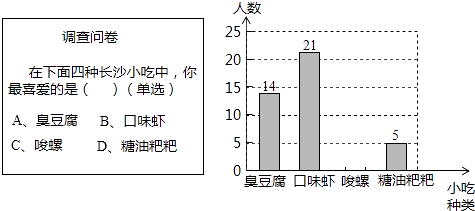
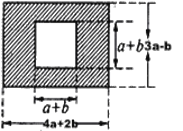
题目内容
【题目】用“※”定义一种新运算:对于任意有理数a和b,规定a※b=ab2+2ab+a.
如:1※2=1×22+2×1×2+1=9
(1)(﹣2)※3= ;
(2)若![]() ※3=16,求a的值;
※3=16,求a的值;
(3)若2※x=m,(![]() x)※3=n(其中x为有理数),试比较m,n的大小.
x)※3=n(其中x为有理数),试比较m,n的大小.
【答案】(1)-32;(2)1;(3)m>n.
【解析】
(1)根据新运算展开,再求出即可;
(2)先根据新运算展开,再解一元一次方程即可;
(3)先根据新运算展开,再求出m、n,即可得出答案.
(1)原式=﹣2×32+2×(﹣2)×3+(﹣2)
=﹣18﹣12﹣2
=﹣32,
故答案为:﹣32.
(2)因为![]() ※3=
※3=![]() ×32+2×
×32+2×![]() ×3+
×3+![]() =8a+8,
=8a+8,
所以8a+8=16,
解得a=1;
(3)根据题意,得m=2x2+2×2x+2=2x2+4x+2,
n=![]() x×32+2×
x×32+2×![]() x×3+
x×3+![]() x=4x,
x=4x,
则m﹣n=2x2+2>0,
所以m>n.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目