题目内容
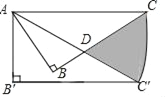
【题目】如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,AC=6,现将Rt△ABC绕点A顺时针旋转30°得到△AB′C′,则图中阴影部分面积为_____.
【答案】3π﹣3![]()
【解析】
根据旋转的性质可得AC′=AC=6,∠CAC′=30°,继而可求得DA=DC,过D作DE⊥AC于E,解直角三角形求得DE长,然后根据扇形和三角形的面积公式进行计算即可求得答案.
∵在Rt△ABC中,∠ABC=90°,∠ACB=30°,AC=6,
∴∠CAB=60°,
∵Rt△ABC绕点A顺时针旋转30°后得到△AB′C′,
∴AC′=AC=6,∠CAC′=30°,
∴∠C′AC=∠ACB,
∴DA=DC,
过D作DE⊥AC于E,
∴CE=![]() AC=3,∠CED=90°,
AC=3,∠CED=90°,
∴DE=CEtan∠ACB=3tan30°=3×![]() =
=![]() ,
,
∴图中阴影部分的面积=S扇形CAC′﹣S△ADC=![]() ﹣
﹣![]() ×6×
×6×![]() =3π﹣3
=3π﹣3![]() ,
,
故答案为:3π﹣3![]() .
.

练习册系列答案
相关题目