题目内容
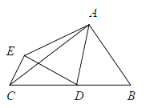
【题目】如图,在△![]() 中,∠
中,∠![]() ,点
,点![]() 是
是![]() 边上一点,以
边上一点,以![]() 为直径的⊙
为直径的⊙![]() 与边
与边![]() 相切于点
相切于点![]() ,与边
,与边![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() ⊥
⊥![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
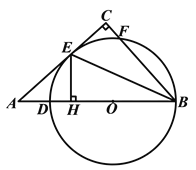
【答案】(1)证明见解析(2)![]()
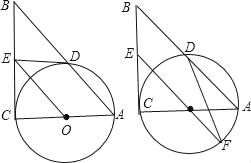
【解析】分析:(1)连接OE.由切线的性质得到OE⊥AC,从而有OE∥BC,由平行线的性质得到∠OEB=∠CBE.再由等腰三角形的性质得到∠OEB=∠OBE,即有∠OBE=∠CBE,由角平分线的性质即可得出结论;
(2)解Rt△ABC得到AB的长.再由OE∥BC,得到△AEO∽△ACB,由相似三角形对应边成比例,得到OB的长,进而可得出结论.
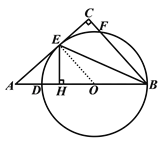
详解:(1)连接OE.
∵⊙O与边AC相切,∴OE⊥AC.
∵∠C=90°,∴OE∥BC,∴∠OEB=∠CBE.
∵OB=OE,∴∠OEB=∠OBE,∴∠OBE=∠CBE.
∵EH⊥AB,∴EH=EC.
(2)在Rt△![]() 中,
中,![]() ,∴
,∴![]() .
.
∵![]() ∥
∥![]() ,∴△AEO∽△ACB,
,∴△AEO∽△ACB,
∴![]() ,即
,即![]() .
.
解得:![]() ,
,
∴![]() .
.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目