题目内容
如图,AB是⊙O的直径,∠B=∠CAD.
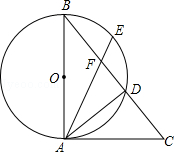
(1)求证:AC是⊙O的切线;
(2)若点E是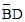 的中点,连接AE交BC于点F,当BD=5,CD=4时,求AF的值.
的中点,连接AE交BC于点F,当BD=5,CD=4时,求AF的值.

(1)求证:AC是⊙O的切线;
(2)若点E是
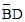 的中点,连接AE交BC于点F,当BD=5,CD=4时,求AF的值.
的中点,连接AE交BC于点F,当BD=5,CD=4时,求AF的值.解:(1)∵AB是⊙O的直径,∴∠ADB=∠ADC=900。
∵∠B=∠CAD,∠C=∠C,∴△ADC∽△BAC。
∴∠BAC=∠ADC=90°。∴BA⊥AC。
又∵AB是⊙O的直径,∴AC是⊙O的切线。
(2)∵△ADC∽△BAC(已证),∴ 。
。
∵BD=5,CD=4,∴BC=9。∴ ,解得:AC=6。
,解得:AC=6。
∴在Rt△ACD中, ,
,
∵∠CAF=∠CAD+∠DAE=∠ABF+∠BAE=∠AFD,
∴CA=CF=6。∴DF=CA-CD=2。
∴在Rt△AFD中, 。
。
∵∠B=∠CAD,∠C=∠C,∴△ADC∽△BAC。
∴∠BAC=∠ADC=90°。∴BA⊥AC。
又∵AB是⊙O的直径,∴AC是⊙O的切线。
(2)∵△ADC∽△BAC(已证),∴
 。
。∵BD=5,CD=4,∴BC=9。∴
 ,解得:AC=6。
,解得:AC=6。∴在Rt△ACD中,
 ,
,∵∠CAF=∠CAD+∠DAE=∠ABF+∠BAE=∠AFD,
∴CA=CF=6。∴DF=CA-CD=2。
∴在Rt△AFD中,
 。
。(1)证明△ADC∽△BAC,可得∠BAC=∠ADC=900,从而可判断AC是⊙O的切线。
(2)根据(1)所得△ADC∽△BAC,可得出CA的长度,从而判断∠CFA=∠CAF,利用等腰三角形的性质得出AF的长度,继而得出DF的长,在Rt△AFD中利用勾股定理可得出AF的长。
(2)根据(1)所得△ADC∽△BAC,可得出CA的长度,从而判断∠CFA=∠CAF,利用等腰三角形的性质得出AF的长度,继而得出DF的长,在Rt△AFD中利用勾股定理可得出AF的长。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



 ﹣1,则△ABC的周长为
﹣1,则△ABC的周长为
 B、6 C、
B、6 C、  D、4
D、4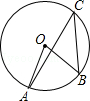
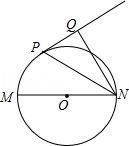
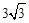 ,求NQ的长.
,求NQ的长.