题目内容
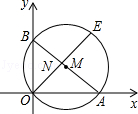
如图,在平面直角坐标系中,以点O为圆心,半径为2的圆与y轴交于点A,点P(4,2)是⊙O外一点,连接AP,直线PB与⊙O相切于点B,交x轴于点C.

(1)证明PA是⊙O的切线;
(2)求点B的坐标;
(3)求直线AB的解析式.

(1)证明PA是⊙O的切线;
(2)求点B的坐标;
(3)求直线AB的解析式.
解;(1)证明:依题意可知,A(0,2),
∵A(0,2),P(4,2),∴AP∥x轴。
∴∠OAP=900,且点A在⊙O上。∴PA是⊙O的切线。
(2)连接OP,OB,作PE⊥x轴于点E,BD⊥x轴于点D,

∵PB切⊙O于点B,∴∠OBP=900,即∠OBP=∠PEC。
又∵OB=PE=2,∠OCB=∠PEC,
∴△OBC≌△PEC(AAS)。∴OC=PC。
设OC=PC=x,则有OE=AP=4,CE=OE-OC=4-x,
在Rt△PCE中,∵PC2=CE2+PE2,即x2=(4-x)2+22,解得x= 。
。
∴BC=CE=4- =
= 。
。
∵ OB·BC=
OB·BC= OC·BD,即
OC·BD,即 ×2×
×2× =
= ×
× ×BD,∴BD=
×BD,∴BD=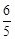 。
。
∴ 。
。
由点B在第四象限可知B( ,
, )。
)。
(3)设直线AB的解析式为y=kx+b,
由A(0,2),B( ,
, ),可得
),可得 ,解得
,解得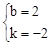 。
。
∴直线AB的解析式为y=-2x+2。
∵A(0,2),P(4,2),∴AP∥x轴。
∴∠OAP=900,且点A在⊙O上。∴PA是⊙O的切线。
(2)连接OP,OB,作PE⊥x轴于点E,BD⊥x轴于点D,

∵PB切⊙O于点B,∴∠OBP=900,即∠OBP=∠PEC。
又∵OB=PE=2,∠OCB=∠PEC,
∴△OBC≌△PEC(AAS)。∴OC=PC。
设OC=PC=x,则有OE=AP=4,CE=OE-OC=4-x,
在Rt△PCE中,∵PC2=CE2+PE2,即x2=(4-x)2+22,解得x=
 。
。∴BC=CE=4-
 =
= 。
。∵
 OB·BC=
OB·BC= OC·BD,即
OC·BD,即 ×2×
×2× =
= ×
× ×BD,∴BD=
×BD,∴BD=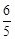 。
。∴
 。
。由点B在第四象限可知B(
 ,
, )。
)。 (3)设直线AB的解析式为y=kx+b,
由A(0,2),B(
 ,
, ),可得
),可得 ,解得
,解得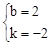 。
。∴直线AB的解析式为y=-2x+2。
试题分析:(1) 点A在圆上,要证PA是圆的切线,只要证PA⊥OA(∠OAP=900)即可,由A、P两点纵坐标相等可得AP∥x轴,所以有∠OAP+∠AOC=1800得∠OAP=900。
(2) 要求点B的坐标,根据坐标的意义,就是要求出点B到x轴、y轴的距离,自然想到构造Rt△OBD,由PB又是⊙O的切线,得Rt△OAP≌△OBP,从而得△OPC为等腰三角形,在Rt△PCE中, PE="OA=2," PC+CE=OE=4,列出关于CE的方程可求出CE、OC的长,△OBC的三边的长知道了,就可求出高BD,再求OD即可求得点B的坐标。
(3)已知点A、点B的坐标用待定系数法可求出直线AB的解析式。

练习册系列答案
相关题目

 cm
cm cm
cm cm
cm


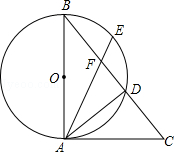
 的中点,连接AE交BC于点F,当BD=5,CD=4时,求AF的值.
的中点,连接AE交BC于点F,当BD=5,CD=4时,求AF的值. 是⊙
是⊙ 的直径,点
的直径,点 、
、 为⊙
为⊙ ,则
,则 的大小为 .
的大小为 .