题目内容
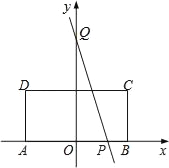
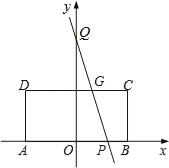
【题目】如图，矩形ABCD的边AB在x轴上，AB的中点与原点O重合，AB＝2，AD＝1，点Q的坐标为（0，2）．点P（x，0）在边AB上运动，若过点Q、P的直线将矩形ABCD的周长分成2：1两部分，则x的值为（ ）
A. 
或-B. 
或-C. 
或-D. 
或-
【答案】D
【解析】
分类讨论：点P在OA上和点P在OB上两种情况．根据题意列出比例关系式，直接解答即可得出x得出值．
如图，∵AB的中点与原点O重合，在矩形ABCD中，AB＝2，AD＝1，
∴A（﹣1，0），B（1，0），C（1，1）．
当点P在OB上时．易求G（
，1）
∵过点Q、P的直线将矩形ABCD的周长分成2：1两部分，
则AP+AD+DG＝3+
x，CG+BC+BP＝3﹣x，
由题意可得：3+x＝2（3﹣x），
解得x＝
．
由对称性可求当点P在OA上时，x＝﹣．
故选：D．
练习册系列答案
相关题目
