题目内容
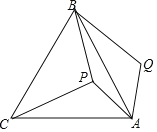
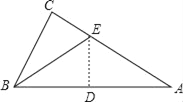
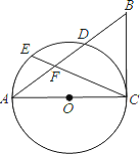
【题目】如图,己知![]() ,以
,以![]() 为直径的
为直径的![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为弧
为弧![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点
于点![]() .且
.且![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() 的半径为4,
的半径为4,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接AE,首先由圆周角定理的推论得出![]() ,则有
,则有![]() ,然后根据等腰三角形的性质和等量代换得出
,然后根据等腰三角形的性质和等量代换得出![]() ,再利用圆周角定理的推论得出
,再利用圆周角定理的推论得出![]() ,则有
,则有![]() ,从而可证
,从而可证![]() ,则结论可证;
,则结论可证;
(2)先结合勾股定理和锐角三角函数求出BC,AB,AF的长度,然后证明![]() ,则有
,则有![]() ,然后设
,然后设![]() ,
,![]() ,在
,在![]() 中利用勾股定理即可求出x的值,进而可求出CE的长度.
中利用勾股定理即可求出x的值,进而可求出CE的长度.
(1)证明:连接![]() ,
,
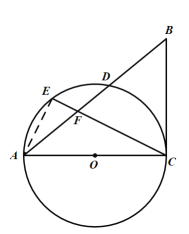
∵![]() 是
是![]() 的直径,
的直径,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]()
∴![]() .
.
∵![]() 为弧
为弧![]() 中点,
中点,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() 为直径,
为直径,
∴![]() 是
是![]() 的切线.
的切线.
(2)解: ∵![]() 的半为4,
的半为4,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
设![]() ,
,![]() ,
,
由勾股定理得:![]() ,
,
解得![]() (负数舍去),
(负数舍去),
∴![]() .
.

【题目】钟南山院士在谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与作答《2020年新型冠状病毒防治全国统一考试(全国卷)》试卷(满分100分),社区管理员随机从甲、乙两个小区各抽取20名人员的答卷成绩,并对他们的成绩(单位:分)进行统计、分析,过程如下:
收集数据
甲小区:80 85 90 95 90 95 90 65 75 100 90 70 95 90 80 80 90 95 60 100
乙小区:60 80 95 80 90 65 80 85 85 100 80 95 90 80 90 70 80 90 75 100
整理数据
成绩 小区 |
|
|
|
|
甲小区 |
|
|
|
|
乙小区 |
|
|
|
|
分析数据
数据名称 计量小区 | 平均数 | 中位数 | 众数 |
甲小区 |
|
|
|
乙小区 |
|
|
|
应用数据
(1)填空:![]() =______,
=______,![]() =______;
=______;
(2)若乙小区共有1200人参与答卷,请估计乙小区成绩大于90分的人数;
(3)社区管理人员看完统计数据,认为甲小区对新型冠状病毒肺炎防护知识掌握更好,请你写出社区管理人员的理由;为了更好地宣传新型冠状病毒肺炎防护知识,社区管理人员决定从甲、乙小区的4个满分试卷中随机抽取两份试卷对小区居民进行网络宣传讲解培训,请用列表格或画树状图的方法求出甲、乙小区各抽到一份满分试卷的概率.