题目内容
【题目】在同一直角坐标系中,抛物线C1:y=ax2﹣2x﹣3与抛物线C2:y=x2+mx+n关于y轴对称,C2与x轴交于A、B两点,其中点A在点B的左侧.
(1)求抛物线C1,C2的函数表达式;
(2)求A、B两点的坐标;
(3)在抛物线C1上是否存在一点P,在抛物线C2上是否存在一点Q,使得以AB为边,且以A、B、P、Q四点为顶点的四边形是平行四边形?若存在,求出P、Q两点的坐标;若不存在,请说明理由.

【答案】(1)C1的函数表示式为y=x2﹣2x﹣3,C2的函数表达式为y=x2+2x﹣3;(2)A(﹣3,0),B(1,0);(3)存在满足条件的点P、Q,其坐标为P(﹣2,5),Q(2,5)或P(2,﹣3),Q(﹣2,﹣3).
【解析】
(1)由对称可求得a、n的值,则可求得两函数的对称轴,可求得m的值,则可求得两抛物线的函数表达式;
(2)由C2的函数表达式可求得A、B的坐标;
(3)由题意可知AB只能为平行四边形的边,利用平行四边形的性质,可设出P点坐标,表示出Q点坐标,代入C2的函数表达式可求得P、Q的坐标.
解:(1)∵C1、C2关于y轴对称,
∴C1与C2的交点一定在y轴上,且C1与C2的形状、大小均相同,
∴a=1,n=﹣3,
∴C1的对称轴为x=1,
∴C2的对称轴为x=﹣1,
∴m=2,
∴C1的函数表示式为y=x2﹣2x﹣3,C2的函数表达式为y=x2+2x﹣3;
(2)在C2的函数表达式为y=x2+2x﹣3中,令y=0可得x2+2x﹣3=0,解得x=﹣3或x=1,
∴A(﹣3,0),B(1,0);
(3)存在.
∵AB只能为平行四边形的一边,
∴PQ∥AB且PQ=AB,
由(2)可知AB=1﹣(﹣3)=4,
∴PQ=4,
设P(t,t2﹣2t﹣3),则Q(t+4,t2﹣2t﹣3)或(t﹣4,t2﹣2t﹣3),
①当Q(t+4,t2﹣2t﹣3)时,则t2﹣2t﹣3=(t+4)2+2(t+4)﹣3,解得t=﹣2,
∴t2﹣2t﹣3=4+4﹣3=5,
∴P(﹣2,5),Q(2,5);
②当Q(t﹣4,t2﹣2t﹣3)时,则t2﹣2t﹣3=(t﹣4)2+2(t﹣4)﹣3,解得t=2,
∴t2﹣2t﹣3=4﹣4﹣3=﹣3,
∴P(2,﹣3),Q(﹣2,﹣3),
综上可知存在满足条件的点P、Q,其坐标为P(﹣2,5),Q(2,5)或P(2,﹣3),Q(﹣2,﹣3).

 千里马走向假期期末仿真试卷寒假系列答案
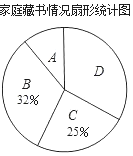
千里马走向假期期末仿真试卷寒假系列答案【题目】在“书香校园”活动中,某校为了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成部分统计图表如下:
类别 | 家庭藏书m本 | 学生人数 |
A | 0≤m≤25 | 20 |
B | 26≤m≤100 | a |
C | 101≤m≤200 | 50 |
D | m≥201 | 66 |
根据以上信息,解答下列问题:
(1)该调查的样本容量为_____,a=_____;
(2)在扇形统计图中,“A”对应扇形的圆心角为_____°;
(3)若该校有2000名学生,请估计全校学生中家庭藏书200本以上的人数.