题目内容
【题目】我们定义:有一组对角相等的四边形叫做“等对角四边形”.
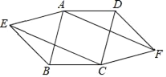
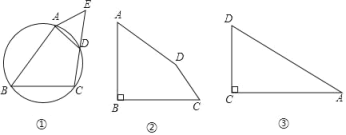
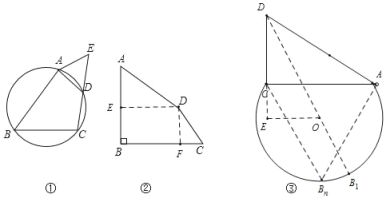
(1)如图①,四边形ABCD内接于⊙O,点E在CD的延长线上,且AE=AD.证明:四边形ABCE是“等对角四边形”.
(2)如图②,在“等对角四边形”ABCD中,∠DAB=∠BCD=53°,∠B=90°,sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() .
.
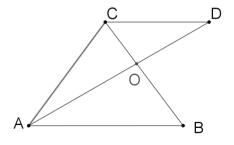
(3)如图③,在Rt△ACD中,∠ACD=90°,∠DAC=30°,CD=4,若四边形ABCD是“等对角四边形”,且∠B=∠D,则BD的最大值是 .(直接写出结果)
【答案】(1)见解析;(2)CD=10;(3)BD的最大值是4![]() +4.
+4.
【解析】
(1)证明∠B=∠E,即可证明四边形ABCE是“等对角四边形”;
(2)过点D作DE⊥AB于点E,DF⊥BC于点F,先证明四边形EBFD为矩形,于是BE=DF,BF=DE,在Rt△CDF中,tan∠FCD=![]() =tan53°=
=tan53°=![]() ,可设DF=4x,CF=3x,则CD=5x, 则BE=DF=4x,DE=BF=18﹣3x,AE=17﹣4x,在Rt△ADE中,∠A=53°,tan∠A=
,可设DF=4x,CF=3x,则CD=5x, 则BE=DF=4x,DE=BF=18﹣3x,AE=17﹣4x,在Rt△ADE中,∠A=53°,tan∠A=![]() ,于是3DE=4AE,列出方程3(18﹣3x)=4(17﹣4x),求得x=2,即CD=5x=10;
,于是3DE=4AE,列出方程3(18﹣3x)=4(17﹣4x),求得x=2,即CD=5x=10;
(3)由∠ABC=60°,可知点B在以AC为边的等边三角形的外接圆的![]() 上运动,当BD经过圆心O时,BD最长,即为B1D的长,求出即可.
上运动,当BD经过圆心O时,BD最长,即为B1D的长,求出即可.
(1)证明:∵四边形ABCD内接于⊙O,
∴∠B+∠ADC=180°,
∵∠ADE+∠ADC=180°,
∴∠B=∠ADE,
∵AE=AD,
∠E=∠ADE,
∴∠B=∠E,
∴四边形ABCE是“等对角四边形”;
(2)如图②,过点D作DE⊥AB于点E,DF⊥BC于点F,
∴∠BED=∠BFD=90°,
又∠B=90°,
∴四边形EBFD为矩形,
∴BE=DF,BF=DE,
在Rt△CDF中,
tan∠FCD=![]() =tan53°=
=tan53°=![]() ,
,
设DF=4x,CF=3x ,则CD=5x
∴BE=DF=4x,DE=BF=18﹣3x,AE=17﹣4x,
在Rt△ADE中,∠A=53°,tan∠A=![]() ,
,
∴3DE=4AE,
3(18﹣3x)=4(17﹣4x),
∴x=2,
CD=5x=10
(3)∵∠ACD=90°,∠DAC=30°,
∴∠CDA=60°,∠ABC=60°,
∴点B在以AC为边的等边三角形的外接圆的![]() 上运动,
上运动,
∴当BD经过圆心O时,BD最长,即为B1D的长,
如图③,连接DO,与弧交于点B1,连接OC,作OE∥AC,与DC的延长线交于点E
∵∠ACD=90°,∠DAC=30°,CD=4,
∴AC=4![]() ,
,
易知∠OCA=30°,∠COE=∠OCA=30°,
∴OC=OB=4,CE=2,OE=![]() ,
,
∴DE=CE+DC=2+4=6
∴OD=![]() ,
,
∴DB1=OD+OB1=4![]() +4,
+4,
则BD的最大值是4![]() +4.
+4.
故答案为4![]() +4.
+4.

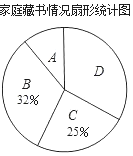
【题目】在“书香校园”活动中,某校为了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成部分统计图表如下:
类别 | 家庭藏书m本 | 学生人数 |
A | 0≤m≤25 | 20 |
B | 26≤m≤100 | a |
C | 101≤m≤200 | 50 |
D | m≥201 | 66 |
根据以上信息,解答下列问题:
(1)该调查的样本容量为_____,a=_____;
(2)在扇形统计图中,“A”对应扇形的圆心角为_____°;
(3)若该校有2000名学生,请估计全校学生中家庭藏书200本以上的人数.