题目内容
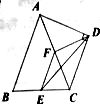
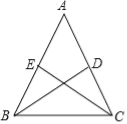
【题目】如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE∥BA交AC于点E,DF∥CA交AB于点F,已知CD=3.
(1)求AD的长;
(2)求四边形AEDF的周长.(注意:本题中的计算过程和结果均保留根号)

【答案】(1)6;(2)![]() .
.
【解析】
试题分析:(1)首先证明∠CAD=30°,易知AD=2CD即可解决问题;
(2)首先证明四边形AEDF是菱形,求出ED即可解决问题;
试题解析:(1)∵∠C=90°,∠B=30°,∴∠CAB=60°,∵AD平分∠CAB,∴∠CAD=![]() ∠CAB=30°,在Rt△ACD中,∵∠ACD=90°,∠CAD=30°,∴AD=2CD=6.
∠CAB=30°,在Rt△ACD中,∵∠ACD=90°,∠CAD=30°,∴AD=2CD=6.
(2)∵DE∥BA交AC于点E,DF∥CA交AB于点F,∴四边形AEDF是平行四边形,∵∠EAD=∠ADF=∠DAF,∴AF=DF,∴四边形AEDF是菱形,∴AE=DE=DF=AF,在Rt△CED中,∵∠CDE=∠B=30°,∴DE=![]() =
=![]() ,∴四边形AEDF的周长为
,∴四边形AEDF的周长为![]() .
.

练习册系列答案
相关题目