Question

【题目】如图，∠BAC的平分线与BC的垂直平分线相交于点D ， DE⊥AB ， DF⊥AC ， 垂足分别为E ， F ， AB=11，AC=5，则BE= ．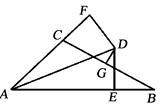

Answer 1

【答案】3
【解析】如图，连接CD，BD，

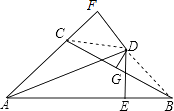
已知AD是∠BAC的平分线，DE⊥AB，DF⊥AC，

根据角平分线的性质可得DF=DE，∠F=∠DEB=90°，∠ADF=∠A

即可得AE=AF，

又因DG是BC的垂直平分线，

所以CD=BD，

在Rt△CDF和Rt△BDE中，CD＝BD，DF＝DE，

利用HL定理可判定DF=DE，Rt△CDF Rt△BDE

由全等三角形的性质可得BE=CF，

所以AB=AE+BE=AF+BE=AC+CF+BE=AC+2BE，

又因AB=11，AC=5，所以BE=3．

首先根据线段的垂直平分线的性质可连接CD、BD，有CD=BD，再根据角平分线的性质可得DF=DE，于是可证Rt△CDF Rt△BDE，由全等三角形的性质可得BE=CF，问题得解。