Question

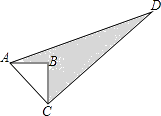
【题目】如图，在已知的△ABC中，按以下步骤作图：
①分别以B，C为圆心，以大于BC的长为半径作弧，两弧相交于两点M，N；
②作直线MN交AB于点D，连接CD．
若CD=AC，∠A=50°，则∠ACB的度数为（　　）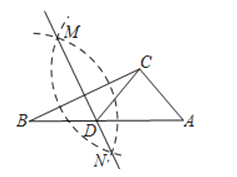

A.90°
B.95°
C.100°
D.105°

Answer 1

【答案】D
【解析】解：∵CD=AC，∠A=50°，
∴∠ADC=∠A=50°，
根据题意得：MN是BC的垂直平分线，
∴CD=BD，
∴∠BCD=∠B，
∴∠B=∠ADC=25°，
∴∠ACB=180°﹣∠A﹣∠B=105°．
故选D．
【考点精析】本题主要考查了线段垂直平分线的性质的相关知识点，需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等才能正确解答此题．