题目内容
【题目】如图,等腰直角三角形ABC,AB=BC,直角顶点B在直线PQ上,且AD⊥PQ于D,CE⊥PQ于E.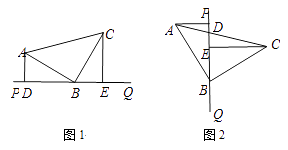
(1)△ADB与△BEC全等吗?为什么?
(2)图1中,AD、DE、CE有怎样的等量关系?说明理由.
(3)将直线PQ绕点B旋转到如图2所示的位置,其他条件不变,那么AD,DE,CE有怎样的等量关系?说明理由.
【答案】
(1)解:△ADB≌△BEC,
理由是:∵AD⊥PQ,CE⊥PQ,
∴∠ADB=∠ABC=∠BEC=90°,
∴∠DAB+∠ABD=90°,∠ABD+∠CBE=90°,
∴∠DAB=∠CBE,
在△ADB和△BEC中,
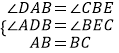
∴△ADB≌△BEC(AAS)
(2)解:CE+AD=DE,
理由是:∵△ADB≌△BEC,
∴AD=BE,CE=DB,
∵DB+BE=DE,
∴CE+AD=DE
(3)解:CE-AD=DE,
理由是:∵AD⊥PQ,CE⊥PQ,
∴∠ADB=∠ABC=∠BEC=90°,
∴∠DAB+∠ABD=90°,∠ABD+∠CBE=90°,
∴∠DAB=∠CBE,
在△ADB和△BEC中,
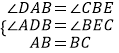
∴△ADB≌△BEC(AAS);
∴AD=BE,CE=DB,
∵DB-BE=DE,
∴CE-AD=DE
【解析】第1小题,根据同角的余角相等可证得∠DAB=∠CBE,用角角边可证△ADB≌△BEC;第2小题,由1知△ADB≌△BEC,于是有AD=BE,CE=DB,所以得CE+AD=DE;第3小题,三条线段的关系是:CE-AD=DE,通过证△ADB≌△BEC可得到。

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目