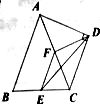
题目内容
【题目】如图,在![]() 中,
中,![]() 分别是
分别是![]() 的中点,以
的中点,以![]() 为斜边作
为斜边作![]() ,若
,若![]() ,则下列结论不正确的是( )
,则下列结论不正确的是( )
A. ![]() B.
B.![]() 平分
平分![]() C.
C. ![]() D.
D.![]()
【答案】C.
【解析】
试题分析:由AB=AC,∠CAB=45°,根据等边对等角及三角形内角和定理求出∠B=∠ACB=67.5°.由Rt△ADC中,∠CAD=45°,∠ADC=90°,根据三角形内角和定理求出∠ACD=45°,根据等角对等边得出AD=DC,那么∠ECD=∠ACB+∠ACD=112.5°,从而判断A正确;根据三角形的中位线定理得到FE=![]() AB,FE∥AB,根据平行线的性质得出∠EFC=∠BAC=45°,∠FEC=∠B=67.5°.根据直角三角形的性质以及等腰三角形的性质得到FD=
AB,FE∥AB,根据平行线的性质得出∠EFC=∠BAC=45°,∠FEC=∠B=67.5°.根据直角三角形的性质以及等腰三角形的性质得到FD=![]() AC,DF⊥AC,∠FDC=45°,等量代换得到FE=FD,再求出∠FDE=∠FED=22.5°,进而判断B正确;
AC,DF⊥AC,∠FDC=45°,等量代换得到FE=FD,再求出∠FDE=∠FED=22.5°,进而判断B正确;
由∠FEC=∠B=67.5°,∠FED=22.5°,求出∠DEC=∠FEC﹣∠FED=45°,从而判断C错误;
在等腰Rt△ADC中利用勾股定理求出AC=![]() CD,又AB=AC,等量代换得到AB=
CD,又AB=AC,等量代换得到AB=![]() CD,从而判断D正确.
CD,从而判断D正确.
∵AB=AC,∠CAB=45°,∴∠B=∠ACB=67.5°.
∵Rt△ADC中,∠CAD=45°,∠ADC=90°,∴∠ACD=45°,AD=DC,
∴∠ECD=∠ACB+∠ACD=112.5°,故A正确,不符合题意;
∵E、F分别是BC、AC的中点,∴FE=![]() AB,FE∥AB,
AB,FE∥AB,
∴∠EFC=∠BAC=45°,∠FEC=∠B=67.5°.
∵F是AC的中点,∠ADC=90°,AD=DC,∴FD=![]() AC,DF⊥AC,∠FDC=45°,
AC,DF⊥AC,∠FDC=45°,
∵AB=AC,∴FE=FD,
∴∠FDE=∠FED=![]() (180°﹣∠EFD)=
(180°﹣∠EFD)=![]() (180°﹣135°)=22.5°,
(180°﹣135°)=22.5°,
∴∠FDE=![]() ∠FDC,∴DE平分∠FDC,故B正确,不符合题意;
∠FDC,∴DE平分∠FDC,故B正确,不符合题意;
∵∠FEC=∠B=67.5°,∠FED=22.5°,
∴∠DEC=∠FEC﹣∠FED=45°,故C错误,符合题意;
∵Rt△ADC中,∠ADC=90°,AD=DC,
∴AC=![]() CD,∵AB=AC,
CD,∵AB=AC,
∴AB=![]() CD,故D正确,不符合题意.
CD,故D正确,不符合题意.
故选C.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案