题目内容
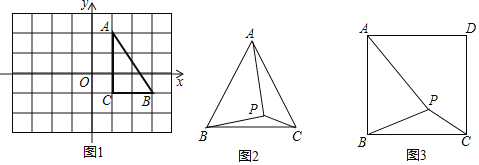
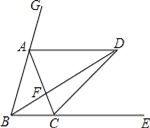
【题目】如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,∠GBE的平分线与AD交于点D,连接CD.
求证:①AB=AD;
②CD平分∠ACE.
【答案】详见解析.
【解析】(1)∵AD∥BE,
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD;
(2)∵AD∥BE,
∴∠ADC=∠DCE,
由①知AB=AD,
又∵AB=AC,
∴AC=AD,
∴∠ACD=∠ADC,
∴∠ACD=∠DCE,
∴CD平分∠ACE;
点睛:角平分线问题的辅助线添加及其解题模型.
①垂两边:如图(1),已知![]() 平分
平分![]() ,过点
,过点![]() 作
作![]() ,
, ![]() ,则
,则![]() .
.
②截两边:如图(2),已知![]() 平分
平分![]() ,点
,点![]()
![]() 上,在
上,在![]() 上截取
上截取![]() ,则
,则![]() ≌
≌![]() .
.
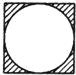
③角平分线+平行线→等腰三角形:
如图(3),已知![]() 平分
平分![]() ,
, ![]() ,则
,则![]() ;
;
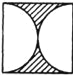
如图(4),已知![]() 平分
平分![]()
![]() ,则
,则![]() .
.
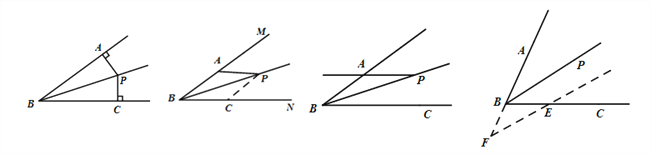
(1) (2) (3) (4)
④三线合一(利用角平分线+垂线→等腰三角形):
如图(5),已知![]() 平分
平分![]() ,且
,且![]() ,则
,则![]() ,
, ![]() .
.
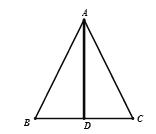
(5)
【题型】解答题
【结束】
26
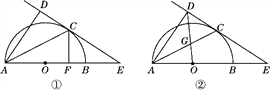
【题目】如图①,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的切线,垂足为D,AB的延长线交直线CD于点E.
(1)求证:AC平分∠DAB;
(2)若AB=4,B为OE的中点,CF⊥AB,垂足为点F,求CF的长;
(3)如图②,连接OD交AC于点G,若![]() ,求sinE的值.
,求sinE的值.
【答案】(1)证明见解析;(2)CF=![]() ;(3) sinE=
;(3) sinE=![]() .
.
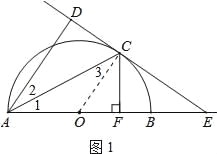
【解析】试题分析:(1)连结OC,如图1,根据切线的性质得OC⊥DE,而AD⊥DE,根据平行线的性质得OC∥AD,所以∠2=∠3,加上∠1=∠3,则∠1=∠2,所以AC平分∠DAB;
(2)如图1,由B为OE的中点,AB为直径得到OB=BE=2,OC=2,在Rt△OCE中,由于OE=2OC,根据含30度的直角三角形三边的关系得∠OEC=30°,则∠COE=60°,由CF⊥AB得∠OFC=90°,所以∠OCF=30°,再根据含30度的直角三角形三边的关系得OF=![]() OC=1,CF=
OC=1,CF=![]() OF=
OF=![]() ;
;
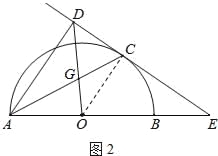
(3)连结OC,如图2,先证明△OCG∽△DAG,利用相似的性质得![]() =
=![]() =
=![]() ,再证明△ECO∽△EDA,利用相似比得到
,再证明△ECO∽△EDA,利用相似比得到![]() =
=![]() =
=![]() ,设⊙O的半径为R,OE=x,代入求得OE=3R;最后在Rt△OCE中,根据正弦的定义求解.
,设⊙O的半径为R,OE=x,代入求得OE=3R;最后在Rt△OCE中,根据正弦的定义求解.
试题解析:(1)连结OC,如图1,∵DE与⊙O切于点C,∴OC⊥DE,
∵AD⊥DE,∴OC∥AD,∴∠2=∠3,∵OA=OC,∴∠1=∠3,
∴∠1=∠2,
即AC平分∠DAB;
(2)如图1,
∵直径AB=4,B为OE的中点,
∴OB=BE=2,OC=2,
在Rt△OCE中,OE=2OC,
∴∠OEC=30°,
∴∠COE=60°,∵CF⊥AB,∴∠OFC=90°,∴∠OCF=30°,∴OF=![]() OC=1,CF=
OC=1,CF=![]() OF=
OF=![]() ;
;
(3)连结OC,如图2,∵OC∥AD,∴△OCG∽△DAG,∴![]() =
=![]() =
=![]() ,∵OC∥AD,
,∵OC∥AD,
∴△ECO∽△EDA,∴![]() =
=![]() =
=![]() ,设⊙O的半径为R,OE=x,∴
,设⊙O的半径为R,OE=x,∴![]() =
=![]() ,解得OE=3R,
,解得OE=3R,
在Rt△OCE中,sin∠E=![]() =
=![]() =
=![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案