题目内容
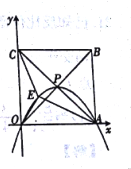
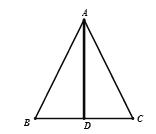
【题目】已知:菱形ABCD中,∠B=60°,将含60°角的直角三角板的60°角的顶点放到菱形ABCD的顶点A处,两边分别与菱形的边BC,CD交于点F,E.
(1)(如图1)求证:AE=AF;
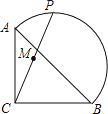
(2)连结EF,交AC于点H(如图2),试探究AB,AF,AH之间的关系;
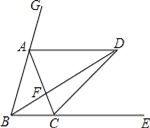
(3)若AB=6,EF=2![]() ,且CE<DE,求FH的长.
,且CE<DE,求FH的长.


【答案】(1)见解析;(2)见解析;(3)![]()
【解析】分析:(1)由菱形的性质得到AD=AC, ∠ACB=∠D,从而用ASA判定出△ACF≌△ADE.
(2)由AE=AF,∠EAF=600,得到△AEF是等边三角形,进而得到∠BAF=∠CAE,从而有△BAF∽△CAH,由相似三角形的性质即可得到结论.
(3)由等边三角形的性质得到AF=EF=AE,再由AF2=AB·AH,得到AH的长,进而得到CH的长,通过证明△CEH∽△DAE,得到![]() ,进而求出CE、EH,FH的长.
,进而求出CE、EH,FH的长.
详解:(1)连结AC.

∵ABCD是菱形,∠B=60°,
∴∠BAD=∠BCD=120°,∠D=60°,
∠ACD=∠ACB=![]() ∠BCD,∠BAC=∠DAC=
∠BCD,∠BAC=∠DAC=![]() ∠BAD.
∠BAD.
∴∠ACB=∠DAC=∠D=60°.
∴AD=AC.
∵∠EAF=60°,∴∠CAF+∠CAE=∠DAE+∠CAE.
∴∠CAF=∠DAE.
∴△ACF≌△ADE.
∴AE=AF.
(2)∵AE=AF,∠EAF=600,∴△AEF是等边三角形.
∴∠AEF=600=∠B.
∴∠BAF+∠CAF=∠CAE+∠CAF=600.
∴∠BAF=∠CAE.
∴△BAF∽△CAH.
∴![]() .∴AB·AH=AE·AF,即AF2=AB·AH.
.∴AB·AH=AE·AF,即AF2=AB·AH.
(3)∵△AEF是等边三角形,∴AF=EF=AE.
∵AF2=AB·AH,AB=6,EF=2![]() ,∴AH=
,∴AH=![]() .
.
∵∠B=∠ACB=600,∴AB=AC=6.
∴CH=AC-AH=6-![]() =
=![]() .
.
∵∠AEF=600,∴∠CEH+∠AED=1200.
∵∠D=600,∴∠DAE+∠AED=1200.
∴∠CEH=∠DAE.
∵∠ACD=∠D=600,∴△CEH∽△DAE.
∴![]() .
.
∵四边形ABCD是菱形,∴AB=BC=CD=AD=6,
∴![]() .∴CE=2或CE=4.
.∴CE=2或CE=4.
∵CE<DE,∴CE=2.
∴![]() .∴EH=
.∴EH=![]() .∴FH=EF-EH=
.∴FH=EF-EH=![]() .
.

 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案