ЬтФПФкШн
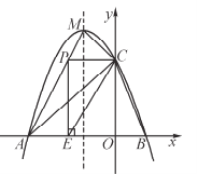
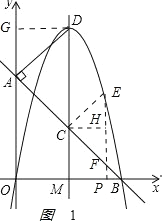
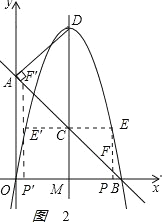
ЁОЬтФПЁПШчЭМЃЌжБЯпABНЛxжсгкЕуBЃЈ2ЃЌ0ЃЉЃЌНЛyжсгкЕуAЃЈ0ЃЌ2ЃЉЃЌжБЯпDMЁЭxжсе§АыжсгкЕуMЃЌНЛЯпЖЮABгкЕуCЃЌDM=3ЃЌСЌНгDAЃЌЁЯDAC=90ЁуЃЎ
ЃЈ1ЃЉЧѓжБЯпABЕФНтЮіЪНЃЎ
ЃЈ2ЃЉЧѓDЕузјБъМАЙ§OЁЂDЁЂBШ§ЕуЕФХзЮяЯпНтЮіЪНЃЎ
ЃЈ3ЃЉШєЕуPЪЧЯпЖЮOBЩЯЕФЖЏЕуЃЌЙ§ЕуPзїxжсЕФДЙЯпНЛABгкFЃЌНЛЃЈ2ЃЉжаХзЮяЯпгкEЃЌСЌCEЃЌЪЧЗёДцдкPЪЙЁїBPFгыЁїFCEЯрЫЦЃПШєДцдкЃЌЧыЧѓГіPЕузјБъЃЛШєВЛДцдкЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉжБЯпABЕФНтЮіЪНЮЊy=Љx+2ЃЛЃЈ2ЃЉDЕузјБъЪЧЃЈ1ЃЌ3ЃЉЃЌХзЮяЯпЕФНтЮіЪНЮЊy=Љ3xЃЈxЉ2ЃЉЃЛЃЈ3ЃЉPЃЈ![]() ЃЌ0ЃЉЃЛЃЈ
ЃЌ0ЃЉЃЛЃЈ![]() ЃЌ0ЃЉЛђЃЈ
ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЃЎ
ЃЌ0ЃЉЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнД§ЖЈЯЕЪ§ЗЈЃЌПЩЕУКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉИљОнЕШбќжБНЧШ§НЧаЮЕФХаЖЈгыаджЪЃЌПЩЕУDЕузјБъЃЌИљОнД§ЖЈЯЕЪ§ЗЈЃЌПЩЕУКЏЪ§НтЮіЪНЃЛ
ЃЈ3ЃЉИљОнЯрЫЦШ§НЧаЮЕФХаЖЈгыаджЪЃЌПЩЕУEЕузјБъЃЌИљОнЕуЕФзјБъТњзуКЏЪ§НтЮіЪНЃЌПЩЕУEЕузјБъЃЌПЩЕУPЕузјБъЃЎ
ЪдЬтНтЮіЃК(1)ЩшжБЯпABЕФНтЮіЪНЮЊy=kx+bЃЌНЋA.BЕузјБъДњШыКЏЪ§НтЮіЪНЃЌЕУ
![]() НтЕУ
НтЕУ![]()
жБЯпABЕФНтЮіЪНЮЊy=x+2ЃЛ
(2)ШчЭМ1ЃЌ
Й§DзїDGЁЭyжсЃЌДЙзуЮЊGЃЌЁпOA=OB=2ЃЌ
ЁрЁїOABЪЧЕШбќжБНЧШ§НЧаЮЁЃ
ЁпADЁЭAB, ![]()
МДЁїADGЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрDG=AG=OGOA=DMOA=32=1ЃЌ
ЁрDЕузјБъЪЧ(1,3)ЃЛ
ЩшХзЮяЯпЕФНтЮіЪНЮЊy=ax(x2)ЃЌНЋDЕузјБъДњШыЃЌЕУ
aЁС1ЁС(12)=3,НтЕУa=3,ХзЮяЯпЕФНтЮіЪНЮЊy=3x(x2)ЃЛ
(3)гЩ(2)ЕУ![]() дђ
дђ![]() ЩшP(x,0)ЃЌMP=x1ЃЌPB=2xЃЌ
ЩшP(x,0)ЃЌMP=x1ЃЌPB=2xЃЌ
ЂйЕБ![]() ЪБ,ЁїBPFЁзЁїFCEЃЌ
ЪБ,ЁїBPFЁзЁїFCEЃЌ
Й§CзїCHЁЭEF, ![]() МДEF=2CH=MPЃЌ
МДEF=2CH=MPЃЌ
ЁрPE=PF+EF=BP+2MP=2x+2(x1)=x,МДE(x,x).
НЋEЕузјБъДњШыХзЮяЯпЃЌЕУ
x=3x(x2)ЃЌ
НтЕУ![]() ЃЈВЛЗћКЯЬтвт,ЩсЃЉ
ЃЈВЛЗћКЯЬтвт,ЩсЃЉ![]() ,МД
,МД![]()
ЂкШчЭМ2ЃЌ
ЕБ![]() ЪБЃЌЁїCEFЁЂЁїBPFЮЊЕШбќжБНЧШ§НЧаЮЃЌPE=MC=1ЃЌ
ЪБЃЌЁїCEFЁЂЁїBPFЮЊЕШбќжБНЧШ§НЧаЮЃЌPE=MC=1ЃЌ
ЁрE(x,1)ЃЌ
НЋEЕузјБъДњШыКЏЪ§НтЮіЪНЃЌЕУ
3x(x2)=1ЃЌ
НтЕУ![]()
ДЫЪБ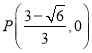 Лђ
Лђ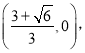
злЩЯЫљЪіЃК ![]()
 Лђ
Лђ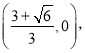

 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ