题目内容
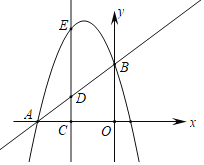
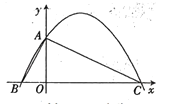
【题目】如图,已知二次函数![]() 的图象与y轴交于点A(0,4),与x轴交于点B,C,点C坐标为(8,0),连接AB,AC.
的图象与y轴交于点A(0,4),与x轴交于点B,C,点C坐标为(8,0),连接AB,AC.
(1)请直接写出二次函数![]() 的解析式.
的解析式.
(2)判断△ABC的形状,并说明理由.
(3)若点N在x轴上运动,当以点A,N,C为顶点的三角形是等腰三角形时,请写出此时点N的坐标.
【答案】(1)![]() ;(2)直角三角形,证明见解析;(3)(3,0)或(-8,0)或(
;(2)直角三角形,证明见解析;(3)(3,0)或(-8,0)或(![]() ,0)或(
,0)或(![]() ,0)
,0)
【解析】
(1)根据待定系数法即可求得;
(2)根据拋物线的解析式求得B的坐标,然后根据勾股定理分别求得AB2=20,AC2=80,BC=10然后根据勾股定理的逆定理即可证得△ABC是直角三角形
(3)分别以A.C两点为圆心,AC长为半径画弧,与m轴交于三个点,由AC的垂直平分线与c轴交于一个点,即可求得点N的坐标
(1)∵二次函数![]() 的图象与y轴交于点A(0,4),与x轴交于点B.C,点C坐标(8,0),
的图象与y轴交于点A(0,4),与x轴交于点B.C,点C坐标(8,0),
∴![]()
解得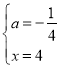
∴抛物线表达式:![]()
△ABC是直角三角形.
令y=0,则![]()
解得x1=8,x2=-2,
∴点B的坐标为(-2,0),
由已知可得,
在Rt△ABO中
AB2=BO2+AO2=22+42=20,
在Rt△AOC中
AC2=AO2+CO2=42+82=80,
又∴BC=OB+OC=2+8=10,
∴在△ABC中
AB2+AC2=20+80=102=BC2
∴△ABC是直角三角形
(3)∵A(0,4),C(8,0),
AC=![]() =4
=4![]() ,
,
①以A为圆心,以AC长为半径作圆,交轴于N,此时N的坐标为(-8,0),
②以C为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为(![]() ,0)或(
,0)或(![]() ,0)
,0)
③作AC的垂直平分线,交g轴于N,此时N的坐标为(3,0),
综上,若点N在轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,点N的坐标分别为(-8,0)、(![]() ,0)、(3,0)、
,0)、(3,0)、![]() ,0)
,0)

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案