题目内容
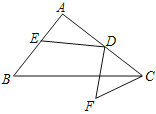
【题目】如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,D为AC中点,E为AB上的动点,将ED绕点D逆时针旋转90°得到FD,连CF,则线段CF的最小值为_____.
【答案】4
【解析】
如图所示,过F作FH⊥AC于H,则∠A=∠DHF=90°,由“AAS”可证△ADE≌△HFD,可得HF=AD=4,当点H与点C重合,线段CF的最小值为4.
如图所示,过F作FH⊥AC于H,则∠A=∠DHF=90°,
∵AC=8,D为AC中点,
∴AD=4,
由旋转可得,DE=DF,∠EDF=90°,
∴∠ADE+∠FDH=90°,∠FDH+∠DFH=90°,
∴∠ADE=∠DFH,且DE=DF,∠A=∠DHF=90°,
∴△ADE≌△HFD(AAS),
∴HF=AD=4,
∴当点H与点C重合,
此时CF=HF=4,
∴线段CF的最小值为4,

故答案为:4

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
【题目】某商场销售一种商品,进价为每件15元,规定每件商品售价不低于进价,且每天销售量不低于90件经调查发现,每天的销售量y(件)与每个商品的售价x(元)满足一次函数关系,其部分数据如下表所示:
每个商品的售价x(元) | … | 30 | 40 | 50 | … |
每天的销售量y(件) | … | 100 | 80 | 60 | … |
(1)填空:y与x之间的函数关系式是______.
(2)设商场每天获得的总利润为w(元),求w与x之间的函数关系式;
(3)不考虑其他因素,当商品的售价为多少元时,商场每天获得的总利润最大,最大利润是多少?