��Ŀ����
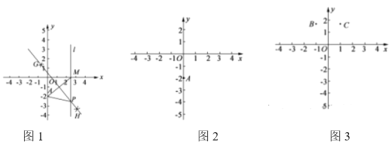
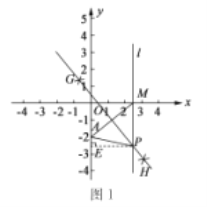
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���A��������![]() ����x������ȡһ��M������AM���ֱ��Ե�A�͵�MΪԲ�ģ�����
����x������ȡһ��M������AM���ֱ��Ե�A�͵�MΪԲ�ģ�����![]() �ij�Ϊ�뾶�����������ཻ��G��H���㣬��ֱ��GH������M��x��Ĵ���l��ֱ��GH�ڵ�P���������ϲ���������������⣮
�ij�Ϊ�뾶�����������ཻ��G��H���㣬��ֱ��GH������M��x��Ĵ���l��ֱ��GH�ڵ�P���������ϲ���������������⣮
̽����
��1���߶�PA��PM��������ϵΪ________��������Ϊ��________________��
��2����x���϶�θı��M��λ�ã���������ͼ�����õ���Ӧ��P�����꣬��������б���
M������ | �� |
|
|
|
| �� |
P������ | �� |
|
| �� |
���룺
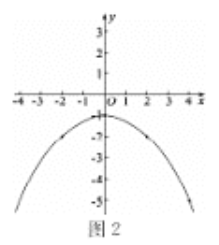
��3�����������������P������꣬����Щ����ƽ����������ͼ2�������������۲컭��������L����������L����״��________��
��֤��
��4�����P��������![]() ������ͼ1���߶�PA��PM�Ĺ�ϵ�����y����x�ĺ�������ʽ��
������ͼ1���߶�PA��PM�Ĺ�ϵ�����y����x�ĺ�������ʽ��
Ӧ�ã�
��5����ͼ3����![]() ��
��![]() �����D��������
�����D��������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���𰸡���1��![]() ���߶δ�ֱƽ�����ϵĵ��������߶������˵�ľ�����ȣ���2��ͼ�������������ߣ���3������������4��
���߶δ�ֱƽ�����ϵĵ��������߶������˵�ľ�����ȣ���2��ͼ�������������ߣ���3������������4��![]() ����5��
����5��![]()
��������
��1���ɳ߹���ͼ�IJ����֪��HG��AM���д��ߣ�����д��ߵ����ʣ����ɵõ��𰸣�
��2�����ݵڣ�1������ͼ�������õ���Ӧ��P��λ�ã�������⣻
��3����ƽ������������ͼ���ɣ�
��4������P��![]() ���ڵ�E���ú�x��y�Ĵ���ʽ��ʾ
���ڵ�E���ú�x��y�Ĵ���ʽ��ʾ![]() ��
��![]() ��
��![]() ����Ϲ��ɶ��������ɵõ��𰸣�
����Ϲ��ɶ��������ɵõ��𰸣�
��5������![]() ��������õ�
��������õ�![]() ʱ����
ʱ����![]() �����Բ�ϣ���
�����Բ�ϣ���![]() ���Ե�Բ�Ľ�Ϊ60�㣬
���Ե�Բ�Ľ�Ϊ60�㣬![]() �����ԲԲ��Ϊ����ԭ��O����
�����ԲԲ��Ϊ����ԭ��O����![]() �����b��ֵ������������⣮
�����b��ֵ������������⣮
�⣺��1��![]() �߶δ�ֱƽ�����ϵĵ��������߶������˵�ľ������
�߶δ�ֱƽ�����ϵĵ��������߶������˵�ľ������
��2��
M������ | �� |
|
|
|
| �� |
P������ | �� |
|
|
|
| �� |
��3����ͼ��ͼ2����״��������
��4����ͼ1������P��![]() ���ڵ�E��
���ڵ�E��
![]() ��
��![]() ��
��![]()
��![]() ��
�У�![]()
��![]()
����![]()
��y����x�ĺ�������ʽΪ![]() ��
��
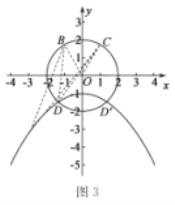
��5������![]() ����
����![]() ����
����![]()
��![]() Ϊ�ȱ������Σ���
Ϊ�ȱ������Σ���![]()
��![]() ʱ����
ʱ����![]() �����Բ�ϣ���
�����Բ�ϣ���![]() ���Ե�Բ�Ľ�Ϊ60��
���Ե�Բ�Ľ�Ϊ60��
��Բ����![]() �Ĵ�ֱƽ����y���ϣ�
�Ĵ�ֱƽ����y���ϣ�
��![]() �����ԲԲ��Ϊ����ԭ��O��
�����ԲԲ��Ϊ����ԭ��O��
��![]() ����
����![]() ����
����![]() ��
��
�ֵ�D�ڸ���������
��![]() ��
��
�ɢ٢�������ã�![]() ����ȥ��
����ȥ��
���ν�Ͽɵã�
��![]() ʱ����D��������
ʱ����D��������![]() ��ȡֵ��ΧΪ
��ȡֵ��ΧΪ
![]()

 ��ʦ�㲦��ϵ�д�
��ʦ�㲦��ϵ�д� Ӣ�żƻ���ĩ����ϵ�д�
Ӣ�żƻ���ĩ����ϵ�д�