题目内容
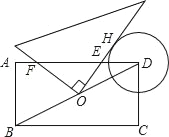
【题目】如图,在矩形ABCD中,AB=2,BC=4,⊙D的半径为1.现将一个直角三角板的直角顶点与矩形的对称中心O重合,绕着O点转动三角板,使它的一条直角边与⊙D切于点H,此时两直角边与AD交于E,F两点,则tan∠EFO的值为_____.
【答案】![]()
【解析】分析: 本题可以通过证明∠EFO=∠HDE,再求出∠HDE的正切值就是∠EFO的正切值.
详解: 连接DH,作OG⊥CD于G,如图,
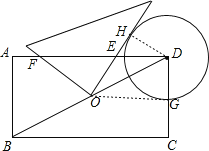
∵在矩形ABCD中,AB=2,BC=4,
∴BD=![]() =2
=2![]() ,
,
∵O是对称中心,
∴OD=![]() BD=
BD=![]() ,
,
∵OG⊥CD,
∴DG=![]() CD=1,OG=
CD=1,OG=![]() BC=2,
BC=2,
∴OG为O的切线,
∵OH是D的切线,
∴DH⊥OH,OH=OG=2,
∵DH=1,
∴tan∠ADB=![]() =
=![]() ,tan∠HOD=
,tan∠HOD=![]() =
=![]() ,
,
∵∠ADB=∠HOD,
∴OE=ED,
设EH为x,则ED=OE=OHEH=2x,
∴1 +x =(2x) ,解得x=![]() ,
,
即EH=![]() .
.
又∵∠FOE=∠DHO=90°,
∴FO∥DH,
∴∠EFO=∠HDE,
∴tan∠EFO=tan∠HDE=![]() =
=![]() .
.
点睛: 本题主要是考查切线的性质及解直角三角形的应用,关键是利用平行把已知角代换成其它相等的容易求出其正切值的角.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目