Question

【题目】已知正方形与正方形（点C、E、F、G按顺时针排列），是的中点，连接，.

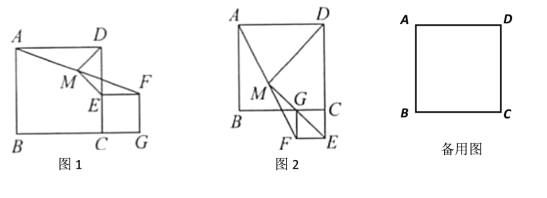
（1）如图1，点在上，点在的延长线上，

求证：=ME，⊥.ME

简析： 由是的中点，AD∥EF，不妨延长EM交AD于点N，从而构造出一对全等的三角形，即 ≌ .由全等三角形性质，易证△DNE是 三角形,进而得出结论.

（2）如图2， 在的延长线上，点在上，（1）中结论是否成立？若成立,请证明你的结论；若不成立，请说明理由.

（3）当AB=5，CE=3时，正方形的顶点C、E、F、G按顺时针排列.若点在直线CD上，则DM= ;若点E在直线BC上，则DM= .

Answer 1

【答案】（1）等腰直角；（2）结论仍成立，见解析；（3）或，.

【解析】

（1）结论：DM⊥EM，DM=EM．只要证明△AMH≌△FME，推出MH=ME，AH=EF=EC，推出DH=DE，因为∠EDH=90°，可得DM⊥EM，DM=ME；
（2）结论不变，证明方法类似；
（3）分两种情形画出图形，理由勾股定理以及等腰直角三角形的性质解决问题即可；

解：（1） △AMN ≌ △FME ,等腰直角.

如图1中，延长EM交AD于H．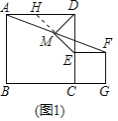

∵四边形ABCD是正方形，四边形EFGC是正方形，
∴，，
∴，
∴，
∵，，
∴△AMH≌△FME，
∴，，
∴，
∵，
∴DM⊥EM，DM=ME．

（2）结论仍成立.

如图，延长EM交DA的延长线于点H,

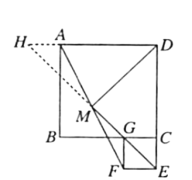
∵四边形ABCD与四边形CEFG都是正方形,

∴，,

∴AD∥EF,∴.

∵，,

∴△AMF≌△FME(ASA), …

∴，,∴.

在△DHE中，，,,

∴，DM⊥EM.

（3）①当E点在CD边上，如图1所示，由（1）的结论可得三角形DME为等腰直角三角形，则DM的长为,此时,所以；

②当E点在CD的延长线上时，如图2所示，由（2）的结论可得三角形DME为等腰直角三角形，则DM的长为，此时 ，所以 ；

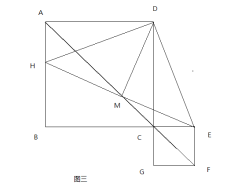
③当E点在BC上是，如图三所示，同（1）、（2）理可得到三角形DME为等腰直角三角形，

证明如下：∵四边形ABCD与四边形CEFG都是正方形, 且点E在BC上

∴AB//EF，∴，

∵M为AF中点，∴AM=MF

∵在三角形AHM与三角形EFM中：

,

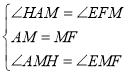∴△AMH≌△FME(ASA),

∴，,∴.

∵在三角形AHD与三角形DCE中：

，

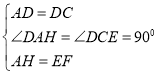∴△AHD≌△DCE(SAS),

∴,

∵∠ADC=∠ADH+∠HDC=90°，

∴∠HDE=∠CDE+∠HDC=90°,

∵在△DHE中，，,,

∴三角形DME为等腰直角三角形，则DM的长为，此时在直角三角形DCE中 ，所以