题目内容
【题目】如图,在平面内有一等腰Rt△ABC,∠ACB=90°,点A在直线l上.过点C作CE⊥1于点E,过点B作BF⊥l于点F,测量得CE=3,BF=2,则AF的长为( )

A. 5 B. 4 C. 8 D. 7
【答案】B
【解析】
过点C作CD⊥BF,交FB的延长线于点D,易证△ACE≌△BCD,根据全等三角形的对应边相等,即可证得AF+BF=2CE,由此即可解决问题。
(1)证明:如图1,过点C作CD⊥BF,交FB的延长线于点D,
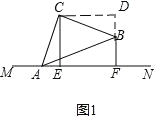
∵CE⊥MN,CD⊥BF,
∴∠CEA=∠D=90°,
∵CE⊥MN,CD⊥BF,BF⊥MN,
∴四边形CEFD为矩形,
∴∠ECD=90°,
又∵∠ACB=90°,
∴∠ACB-∠ECB=∠ECD-∠ECB,
即∠ACE=∠BCD,
又∵△ABC为等腰直角三角形,
∴AC=BC,
在△ACE和△BCD中,
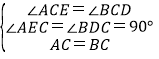 ,
,
∴△ACE≌△BCD(AAS),
∴AE=BD,CE=CD,
又∵四边形CEFD为矩形,
∴四边形CEFD为正方形,
∴CE=EF=DF=CD,
∴AF+BF=AE+EF+BF
=BD+EF+BF
=DF+EF
=2CE,
∵CE=3,BF=2,
∴AF=6-2=4.
故选B.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目