题目内容
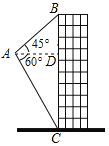
【题目】如图,![]() ,作
,作![]() 垂足为点
垂足为点![]() ,
,![]() 相交于点
相交于点![]() .
.
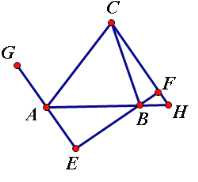
(1)求![]() 的度数.
的度数.
(2)求证:![]()
【答案】(1)∠E=90°;(2)见解析.
【解析】
(1)根据三角形外角的性质和角平分线的定义可得∠CAB+∠CBA=90°+![]() ∠E,然后在△ABC中利用三角形内角和定理可列式求出∠E;
∠E,然后在△ABC中利用三角形内角和定理可列式求出∠E;
(2)根据等角的余角相等可证∠BHC=∠BAE.
解:(1)∵∠GAB=∠E+∠ABE,∠ABF=∠E+∠BAE,
∴∠GAB+∠ABF=∠E+∠ABE+∠E+∠BAE=∠E+180°,
∵![]()
∴∠CAB=![]() ∠GAB,∠CBA=
∠GAB,∠CBA=![]() ∠ABF,
∠ABF,
∴∠CAB+∠CBA=![]() (∠GAB+∠ABF)=90°+
(∠GAB+∠ABF)=90°+![]() ∠E,
∠E,
∵∠CAB+∠CBA+∠ACB=180°,即90°+![]() ∠E+45°=180°,
∠E+45°=180°,
∴∠E=90°;
(2)∵CF⊥BF,
∴∠BFH=90°,
∴∠FBH+∠BHC=90°,
∵∠E=90°,
∴∠BAE+∠ABE=90°,
又∵∠ABE=∠FBH,
∴∠BHC=∠BAE.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
【题目】甲、乙两名学生进行射击练习,两人在相同条件下各射击10次,将射击结果作统计分析如下:
命中环数 | 5 | 6 | 7 | 8 | 9 | 10 |
甲命中环数的次数 | 1 | 4 | 2 | 1 | 1 | 1 |
乙命中环数的次数 | 1 | 2 | 4 | 2 | 1 | 0 |
平均数 | 众数 | 方差 | |
甲 | 7 | 6 | 2.2 |
乙 |
(1)请你计算乙学生的相关数据并填入表中;
(2)根据你所学的统计学知识,利用上述某些数据评价甲、乙两人的射击水平。