题目内容
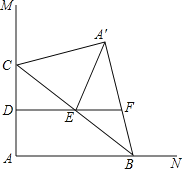
【题目】如图,∠MAN=90°,点C在边AM上,AC=4,点B为边AN上一动点,连接BC,△A′BC与△ABC关于BC所在直线对称,点D,E分别为AC,BC的中点,连接DE并延长交A′B所在直线于点F,连接A′E.当△A′EF为直角三角形时,AB的长为_____.
【答案】![]() 或4
或4
【解析】当△A′EF为直角三角形时,存在两种情况:
①当∠A'EF=90°时,如图1,根据对称的性质和平行线可得:A'C=A'E=4,根据直角三角形斜边中线的性质得:BC=2A'B=8,最后利用勾股定理可得AB的长;
②当∠A'FE=90°时,如图2,证明△ABC是等腰直角三角形,可得AB=AC=4.
当△A′EF为直角三角形时,存在两种情况:
①当∠A'EF=90°时,如图1,
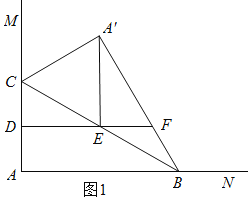 .
.
∵△A′BC与△ABC关于BC所在直线对称,
∴A'C=AC=4,∠ACB=∠A'CB,
∵点D,E分别为AC,BC的中点,
∴D、E是△ABC的中位线,
∴DE∥AB,
∴∠CDE=∠MAN=90°,
∴∠CDE=∠A'EF,
∴AC∥A'E,
∴∠ACB=∠A'EC,
∴∠A'CB=∠A'EC,
∴A'C=A'E=4,
Rt△A'CB中,∵E是斜边BC的中点,
∴BC=2A'E=8,
由勾股定理得:AB2=BC2-AC2,
∴AB=![]() ;
;
②当∠A'FE=90°时,如图2,
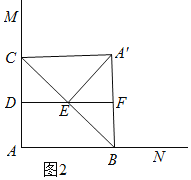 .
.
∵∠ADF=∠A=∠DFB=90°,
∴∠ABF=90°,
∵△A′BC与△ABC关于BC所在直线对称,
∴∠ABC=∠CBA'=45°,
∴△ABC是等腰直角三角形,
∴AB=AC=4;.
综上所述,AB的长为4![]() 或4;
或4;
故答案为:4![]() 或4.
或4.

 阅读快车系列答案
阅读快车系列答案【题目】有20筐白菜,以每筐25千克为标准,超过或不足的分别用正、负数来表示.记录如下(单位:千克):
与标准质量的差 | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)这些白菜中,最重的一筐比最轻的一筐重多少千克?
(2)与标准重量比较,20筐白菜总计为超过或不足多少千克?
(3))若白菜每千克售价2.6元,则这20筐白菜可卖多少元?