题目内容
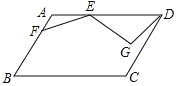
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,且AD//BC,BD的垂直平分线经过点O,分别与AD、BC交于点E、F
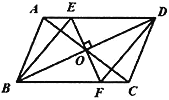
(1)求证:四边形ABCD为平行四边形;
(2)求证:四边形BFDE为菱形.
【答案】(1)见解析;(2)见解析.
【解析】
(1)由平行线的性质可得![]() ,根据EF经过点O且垂直平分BD可得
,根据EF经过点O且垂直平分BD可得![]() ,利用ASA可证明△DOA≌△BOC,可得OA=OC,即可证明四边形ABCD为平行四边形;
,利用ASA可证明△DOA≌△BOC,可得OA=OC,即可证明四边形ABCD为平行四边形;
(2)利用ASA可证明![]() ≌
≌![]() ,可得OE=OF,根据对角线互相垂直且平分的四边形是菱形即可得结论.
,可得OE=OF,根据对角线互相垂直且平分的四边形是菱形即可得结论.
(1)∵AD//BC,![]() 经过点O,且垂直平分
经过点O,且垂直平分![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 和
和![]() 中
中 ,
,
∴![]() ≌
≌![]() ,
,
∴OA=OC,
∴四边形![]() 为平行四边形.
为平行四边形.
(2)由(1)知![]() ,
,![]() ,
,
∴在![]() 和
和![]() 中
中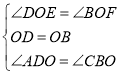 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
∵![]() 垂直平分
垂直平分![]() ,
,
∴![]() ,
,![]() ,
,
∴四边形![]() 为菱形.
为菱形.

练习册系列答案
相关题目
【题目】甲、乙两人参加射击比赛,每人射击五次,命中的环数如下表:
次序 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次 |
甲命中的环数(环) | 6 | 7 | 8 | 6 | 8 |
乙命中的环数(环) | 5 | 10 | 7 | 6 | 7 |
根据以上数据,下列说法正确的是( )
A.甲的平均成绩大于乙B.甲、乙成绩的中位数不同
C.甲、乙成绩的众数相同D.甲的成绩更稳定