题目内容
【题目】如图,平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点E在AD上,且AE=4,点
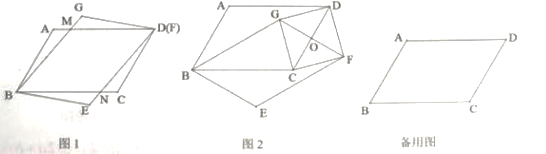
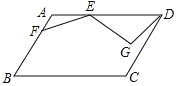
,点E在AD上,且AE=4,点![]() 是AB上一点,连接EF,将线段EF 绕点E逆时针旋转120°得到EG,连接DG,则线段DG的最小值为____________________.
是AB上一点,连接EF,将线段EF 绕点E逆时针旋转120°得到EG,连接DG,则线段DG的最小值为____________________.
【答案】![]()
【解析】
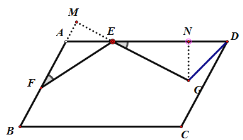
结合已知条件,作出辅助线,通过全等得出ME=GN,且随着点F的移动,ME的长度不变,从而确定当点N与点D重合时,使线段DG最小.
解:如图所示,过点E做EM⊥AB交BA延长线于点M,过点G作GN⊥AD交AD于点N,
∴∠EMF=∠GNE=90°
∵四边形ABCD是平行四边形,BC=12
∴AD∥BC,AD=BC=12,
∴∠BAD=120°,
∴∠AFE+∠AEF=60°
又∵EG为EF逆时针旋转120°所得,
∴∠FEG=120°,EF=EG,
∴∠AEF+∠GEN=60°,
∴∠AFE=∠GEN,
∴在△EMF与△GNE中,∠AFE=∠GEN,∠EMF=∠GNE=90°,EF=EG,
∴△EMF≌△GNE(AAS)
∴ME=GN
又∵∠EAM=∠B=60°,AE=4,
∴∠AEM=30°,![]() ,
,![]() ,
,
∴![]() ,
,
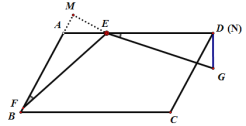
∴当点N与点D重合时,使线段DG最小,如图所示,此时![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目