Question

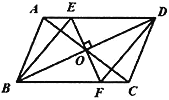
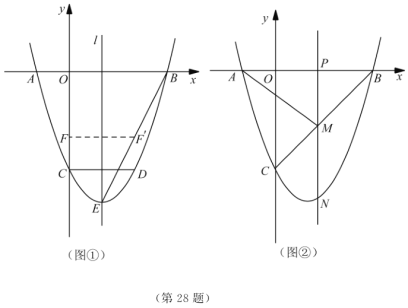
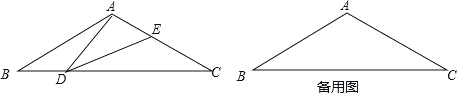
【题目】已知：如图12①、②、③，在矩形ABCD中，AB＝4，BC＝8，P是边BC上的一个动点．

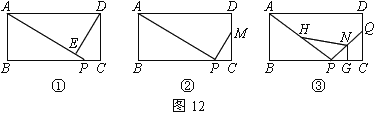
（1）如图①，若DE⊥AP，垂足为E，求证：△AED∽△PBA

（2）如图②，在（1）的条件下，将DE沿AP方向平移，使P、E两点重合，且与边CD的交点为M，若MC＝3，求BP的长．

（3）如图③，Q是边CD上的一个动点，若＝2，且H，N，G分别为AP，PQ，PC的中点，请问：在P、Q两点分别在BC、CD上运动的过程中，四边形HPGN的面积是否发生变化？若变化，请说明理由，若不变化，请求出它的面积．

Answer 1

【答案】（1）见解析；（2）BP的长为2或6；（3）四边形HPGN的面积不会发生变化，它的面积是4

【解析】

(1)根据题意知∠DAE=∠APB，利用DE⊥AP，∠B=90°，即可得到△AED∽△PBA；

(2)根据题意可以证得△APB∽△PMC，设BP=x，则PC=8-x，利用相似的性质=，将对应的线段值代入进去，列出方程即可求解；

(3)根据题意设设CQ=k，则BP=2k，过点H作HF⊥BC于F，可证得△PHF∽△PAB，得出HF=AB=2，PF=PB=k，利用三角形中位线性质可得△PNG∽△PQC，得出PG=4-k，NG=4，从而表示出四边形HPGN的面积即可.

证明：(1)∵四边形ABCD是矩形，

∴AD∥BC，∠B=90°，

∴∠DAE=∠APB．

又∵DE⊥AP，

∴∠DEA=90°，

∴∠DEA=∠B，

∴△AED∽△PBA．

(2)由题意知MP⊥AP，

∴∠APM=90°，

∴∠APB+∠MPC=90°．

又∵∠APB+∠PAB=90°，

∴∠APB=∠PMC．

∵∠B=∠C=90°，

∴△APB∽△PMC，

∴=．

设BP=x，则PC=8-x，

∴=，

解得x=2或6，

∴BP的长为2或6．

（3）因为=2，设CQ=k，则BP=2k．

如图，过点H作HF⊥BC于F，

又∵AB⊥BC，

∴HF∥AB，

∴△PHF∽△PAB，

∴===，

∴HF=AB=2，PF=PB=k．

∵N、G分别是PQ，PC的中点，

∴NG∥QC，

∴△PNG∽△PQC，

∴===，

∴PG=PC=( BC-BP)=4-k，NG=CQ=k．

∴S四边形HPGN=S梯形HFGN-S△HFP=(k+2)(4-k+k)-×2k=k+4-k=4．

所以，四边形HPGN的面积不会发生变化，它的面积是4．