Question

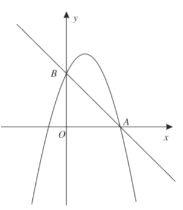
【题目】已知一次函数与二次函数的图象的一个交点坐标为，另一个交点在轴上，点为轴右侧抛物线上的一动点．

（1）求此二次函数的解析式；

（2）当点位于直线上方的抛物线上时，求面积的最大值；

（3）当此抛物线在点与点之间的部分（含点和点）的最高点与最低点的纵坐标之差为9时，请直接写出点的坐标和的面积．

Answer 1

【答案】（1）；（2）最大值；（3），．

【解析】

（1）先把A点坐标代入一次函数的解析式求出k，再求出B点坐标，把A、B两点坐标代入抛物线解析式即可求解；

（2）过作轴交于点，设点坐标为，则C(m，-m+3)，表示出PC，根据求解，配方即可求得最大值；

（3）先分析出P点在对称轴的右侧，则其最高点为顶点，其纵坐标为4，根据最高点与最低点的纵坐标之差为9，求出P点的纵坐标，代入函数解析式即可求出横坐标，过P点作PD平行于y轴，交AB于D点，根据求解即可．

（1）∵点在一次函数的图象上，

∴

∴

∴一次函数的解析式为，

∴

又∵、都在二次函数的图像上，

∴

∴，

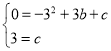
∴二次函数的解析式为

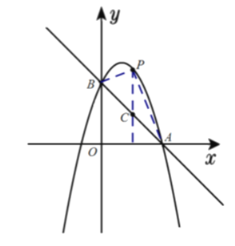
（2）过作轴交于点，设点坐标为

则，

∴

∴

∵

∴当时，有最大值

（3）∵二次函数的解析式为

∴抛物线的最高点的纵坐标为4

∵，点为轴右侧，在点与点之间的部分（含点和点）的最高点与最低点的纵坐标之差为9

∴P点在对称轴的右侧，其纵坐标为4-9=-5

把y=-5代入得：x=4

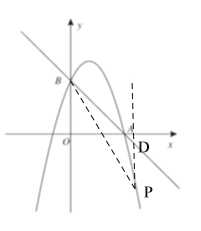
∴p点的坐标为

过P点作PD平行于y轴，交AB于D点，则D的坐标为(4，-1)

∴PD=4

∴=