题目内容
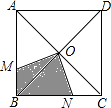
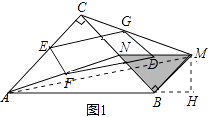
【题目】如图1,在△ABC和△MNB中,∠ACB=∠MBN=90°,AC=BC=4,MB=NB= ![]() BC,点N在BC边上,连接AN,CM,点E,F,D,G分别为AC,AN,MN,CM的中点,连接EF,FD,DG,EG.
BC,点N在BC边上,连接AN,CM,点E,F,D,G分别为AC,AN,MN,CM的中点,连接EF,FD,DG,EG. 
(1)判断四边形EFDG的形状,并证明;
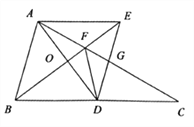
(2)如图2,将图1中的△MBN绕点B逆时针旋转90°,其他条件不变,猜想此时四边形EFDG的形状,并证明. 
【答案】
(1)解:四边形EFDG是平行四边形,
理由:如图1,连接AM,
∵E、F、D、G分别为AC、AN、MN、CM的中点,
∴FD=EG= ![]() AM,EF=GD=
AM,EF=GD= ![]() CN,
CN,
∴四边形EFDG是平行四边形;
(2)解:四边形EFDG是正方形,
理由:如图2,连接CN,AM,分别交EF、CN于点L与K,
由已知得:点M和点D分别落在BC与AB边上,
∴CM=CB﹣BM=4﹣2=2,
∴CM=BN,
∵∠ACM=∠CBN=90°,AC=BC,
∴△ACM≌△CBN(SAS),
∴AM=CN,∠CAM=∠BCN,
∵∠ACK+∠KCM=90°,
∴∠ACK+∠CAK=90°,
在△ACK中,∠AKC=180°﹣(∠ACK+∠CAK)=180°﹣90°=90°,
由(1)可得EG∥AM∥FD,EF∥CN∥GD,
∴四边形EFDG是平行四边形,
∴∠GEL=∠ELA=∠AKC=90°,
∴四边形EFDG是矩形,
∵EG= ![]() AM=
AM= ![]() CN=EF,
CN=EF,
∴四边形EFDG是正方形.

【解析】(1)四边形EFDG是平行四边形,理由为:如图1,连接AM,由E、F、G、H分别为中点,利用利用中位线定理得到两组对边相等,即可得证;(2)四边形EFDG为正方形,理由为:如图2,连接CN,AM,分别交EF、CN于点L与K,由CB﹣BM求出CM的长,得到CM=BN,再由一对直角相等,AC=BC,利用SAS得到三角形ACM与三角形CBN全等,利用全等三角形对应边、对应角相等得到AM=CN,∠CAM=∠BCN,利用同角的余角相等,求出∠AKC为直角,利用两组对边平行的四边形为平行四边形得到四边形EFDG为平行四边形,再由一个内角为直角,且邻边相等即可得证.
【考点精析】通过灵活运用等腰直角三角形和三角形中位线定理,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半即可以解答此题.