题目内容
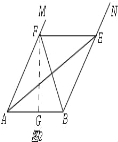
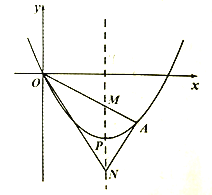
【题目】如图,矩形ABCD中,AD=3厘米,AB=a厘米(a>3).动点M,N同时从B点出发,分别沿B→A,B→C运动,速度是1厘米/秒.过M作直线垂直于AB,分别交AN,CD于P,Q.当点N到达终点C时,点M也随之停止运动.设运动时间为t秒.

(1)若a=4厘米,t=1秒,则PM=______厘米;
(2)若a=5厘米,求时间t,使△PNB∽△PAD,并求出它们的相似比;
(3)若在运动过程中,存在某时刻使梯形PMBN与梯形PQDA的面积相等,求a的取值范围;
【答案】(1)![]() ;(2)2∶3;(3)3<a≤6.
;(2)2∶3;(3)3<a≤6.
【解析】
(1)由题意可知,t=1秒时,BN=BM=1,又因为PM⊥BC,所以△ANB∽△APM,根据相似三角形的性质,即可求得PM;(2)根据题意,当△PNB∽△PAD时,对应边之比等于高之比,即![]() 进而可以求出时间t以及相似比;(3)设BN=t,则0
进而可以求出时间t以及相似比;(3)设BN=t,则0![]() ,则BM=t,再用t表示出PM,就可以用t表示出两个梯形的面积,求出t的值,进而求出a的取值范围.
,则BM=t,再用t表示出PM,就可以用t表示出两个梯形的面积,求出t的值,进而求出a的取值范围.
解:(1)当t=1时,MB=1,NB=1,AM=4-1=3,
∵PM∥BN,
∴△ANB∽△APM,
∴![]() ,
,
∴PM=![]() .
.
(2)作出△PNB和△PAD,则BM和AM分别是它们的高,
若△PNB∽△PAD,则![]() ,
,
即![]() ,解得t=2,
,解得t=2,
即t=2时,使得△PNB∽△PAD,
∴相似比为2∶3.
(3)∵PM⊥AB,CB⊥AB,∠AMP=∠ABC,△AMP∽△ABN,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
当梯形PMBN与梯形PQDA的面积相等时,
即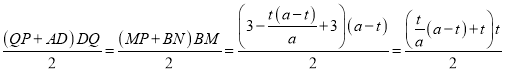 ,
,
化简得t=![]() ,
,
∵t![]() 3,
3,
∴![]() ,则a
,则a![]() 6,
6,
∴3![]() a
a![]() 6.
6.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目