题目内容
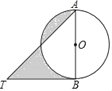
【题目】如图,AB是⊙O的直径,BT是⊙O的切线,若∠ATB=45°,AB=2,则阴影部分的面积是_____.
【答案】1
【解析】
设AT与圆O相交于点C,连接BC,根据切线的性质得到AB⊥TB,因为∠ATB=45°,得到∠TAB=45°=∠ATB,根据等腰直角三角形的性质得到AB=TB=2,根据直径所对的圆周角是直角得到∠ACB=90°,推出∠CAB=∠CBA=45°=∠ATB,AC=BC=TC,点C是弧ACB的中点,则S阴影=S△TCB,即可求解.
解:如图:设AT与圆O相交于点C,连接BC

∵BT是⊙O的切线
∴AB⊥TB,
又∵∠ATB=45°
∴∠TAB=45°=∠ATB
∴AB=TB=2
∵AB是直径
∴∠ACB=90°
∴∠CAB=∠CBA=45°=∠ATB
∴AC=BC=TC
∴点C是![]() 的中点
的中点
∴S阴影=S△TCB
∴S阴影=![]() S△ABT
S△ABT![]()
故答案为:1

练习册系列答案
相关题目
【题目】某一天,水果经营户老张用1600元从水果批发市场批发猕猴桃和芒果共50千克,后再到水果市场去卖,已知猕猴桃和芒果当天的批发价和零售价如表所示:
品名 | 猕猴桃 | 芒果 |
批发价 | 20 | 40 |
零售价 | 26 | 50 |
![]() 他购进的猕猴桃和芒果各多少千克?
他购进的猕猴桃和芒果各多少千克?
![]() 如果猕猴桃和芒果全部卖完,他能赚多少钱?
如果猕猴桃和芒果全部卖完,他能赚多少钱?
【题目】某校两次购买足球和篮球的支出情况如表:
足球(个) | 篮球(个) | 总支出(元) | |
第一次 | 2 | 3 | 310 |
第二次 | 5 | 2 | 500 |
(1)求购买一个足球、一个篮球的花费各需多少元?(请列方程组求解)
(2)学校准备给帮扶的贫困学校送足球、篮球共计60个,恰逢市场对两种球的价格进行了调整,足球售价提高了10%,篮球售价降低了10%,如果要求一次性购得这批球的总费用不超过4000元,那么最多可以购买多少个足球?