题目内容
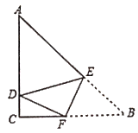
【题目】如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DE上,点A,D,G在同一直线上,且AD=3,DE=1,连接AC,CG,AE,并延长AE交CG于点H.
(1)求sin∠EAC的值.
(2)求线段AH的长.
【答案】(1)、![]() ;(2)、
;(2)、![]()
【解析】
试题分析:(1)、作EM⊥AC于M,根据sin∠EAM=![]() 求出EM、AE即可解决问题;(2)、先证明△GDC≌△EDA,得∠GCD=∠EAD,推出AH⊥GC,再根据S△AGC=
求出EM、AE即可解决问题;(2)、先证明△GDC≌△EDA,得∠GCD=∠EAD,推出AH⊥GC,再根据S△AGC=![]() AGDC=
AGDC=![]() GCAH,即可解决问题.
GCAH,即可解决问题.
试题解析:(1)、作EM⊥AC于M. ∵四边形ABCD是正方形, ∴∠ADC=90°,AD=DC=3,∠DCA=45°,
∴在RT△ADE中,∵∠ADE=90°,AD=3,DE=1, ∴AE=![]() =
=![]() ,
,
在RT△EMC中,∵∠EMC=90°,∠ECM=45°,EC=2, ∴EM=CM=![]() ,
,
∴在RT△AEM中,sin∠EAM=![]() =
=![]() =
=![]() .
.
(2)、在△GDC和△EDA中,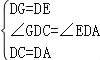 , ∴△GDC≌△EDA, ∴∠GCD=∠EAD,GC=AE=
, ∴△GDC≌△EDA, ∴∠GCD=∠EAD,GC=AE=![]() ,
,
∵∠EHC=∠EDA=90°, ∴AH⊥GC, ∵S△AGC=![]() AGDC=
AGDC=![]() GCAH, ∴
GCAH, ∴![]() ×4×3=
×4×3=![]() ×
×![]() ×AH,
×AH,
∴AH=![]()
![]() .
.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案【题目】某校开展校园“美德少年”评选活动,共有“助人为乐”,“自强自立”、“孝老爱亲”,“诚实守信”四种类别,每位同学只能参评其中一类,评选后,把最终入选的20位校园“美德少年”分类统计,制作了如下统计表,后来发现,统计表中前两行的数据都是正确的,后两行的数据中有一个是错误的.
类别 | 频数 | 频率 |
助人为乐美德少年 | a | 0.20 |
自强自立美德少年 | 3 | b |
孝老爱亲美德少年 | 7 | 0.35 |
诚实守信美德少年 | 6 | 0.32 |
根据以上信息,解答下列问题:
(1)统计表中的a= ,b ;
(2)统计表后两行错误的数据是 ,该数据的正确值是 ;
(3)校园小记者决定从A,B,C三位“自强自立美德少年”中随机采访两位,用画树状图或列表的方法,求A,B都被采访到的概率.