Question

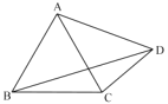
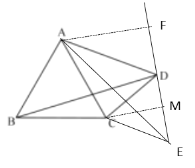
【题目】如图，点为等边外一点，，连接，若，的面积为，则的长为_____________．

Answer 1

【答案】

【解析】

作等边△CDE，延长ED，作AF⊥ED，过点C作CM⊥DE，根据SAS定理证明△BCD≌△ACE，从而得到，然后根据题意判定AD∥CE，从而得到，然后根据含30°直角三角形的性质结合三角形的面就，求得，DF=,从而求得DE和AF的长度，然后利用勾股定理求解．

解：作等边△CDE，延长ED，作AF⊥ED，过点C作CM⊥DE

由题意可知：∠ACB=∠ECD=60°，AC=AB，DC=EC

∴∠ACB+∠ACD=∠ECD+∠ACD

∴∠BCD=∠ACE

∴△BCD≌△ACE

∴BD=AE，

∵∠DCE=∠ADC=60°

∴AD∥CE

∴

∴，

解得：DE=5

又∵∠ADC=∠CDE=60°

∴∠ADF=60°

∴在Rt△ADF中，∠DAF=30°

∴DF=,

∴EF=5+4=9

在Rt△AEF中，

∴BD=

故答案为：．