题目内容
【题目】在矩形ABCD中，M，N，P，Q分别为边AB，BC，CD，DA上的点（不与端点重合）．
对于任意矩形ABCD，下面四个结论中，①存在无数个四边形MNPQ是平行四边形；②存在无数个四边形MNPQ是矩形；③存在无数个四边形MNPQ是菱形；④至少存在一个四边形MNPQ是正方形．所有正确结论的序号是______．
【答案】①②③
【解析】
根据矩形的判定和性质，菱形的判定，正方形的判定，平行四边形的判定定理即可得到结论．
解：
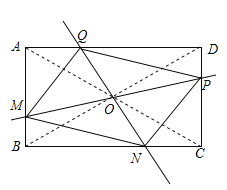
①如图，∵四边形ABCD是矩形，连接AC，BD交于O，
过点O直线MP和QN，分别交AB，BC，CD，AD于M，N，P，Q，
则四边形MNPQ是平行四边形，
故当MQ∥PN，PQ∥MN，四边形MNPQ是平行四边形，
故存在无数个四边形MNPQ是平行四边形；故正确；
②如图，当PM=QN时，四边形MNPQ是菱形，故存在无数个四边形MNPQ是矩形；故正确；
③如图，当PM⊥QN时，存在无数个四边形MNPQ是菱形；故正确；
④当四边形MNPQ是正方形时，MQ=PQ，
则△AMQ≌△DQP，
∴AM=QD，AQ=PD，
∵PD=BM，
∴AB=AD，
∴四边形ABCD是正方形与任意矩形ABCD矛盾，故错误；
故答案为：①②③．
名校课堂系列答案
【题目】一辆汽车油箱中有汽油
.如果不再加油，那么油箱中的油量
（单位：
）随行驶路程
（单位：
）的增加而减少.已知该汽车平均耗油量为
.
（Ⅰ）计算并填写下表：
| 10 | 100 | 300 | … |
| … |
（Ⅱ）写出表示与的函数关系式，并指出自变量的取值范围；
（Ⅲ）若
，
两地的路程约有
，当油箱中油量少于
时，汽车会自动报警，则这辆汽车在由地到
地，再由地返回地的往返途中，汽车是否会报警？请说明理由.
【题目】为了推动全社会自觉尊法学法守法用法，促进全面依法治国，某区每年都举办普法知识竞赛，该区某单位甲、乙两个部门各有员工200人，要在这两个部门中挑选一个部门代表单位参加今年的竞赛，为了解这两个部门员工对法律知识的掌握情况，进行了抽样调查，从甲、乙两个部门各随机抽取20名员工，进行了法律知识测试，获得了他们的成绩（百分制），并对数据（成绩）进行整理，描述和分析，下面给出了部分信息．
a．甲部门成绩的频数分布直方图如下（数据分成6组：40≤x＜50，50≤x＜60，60≤x＜70，70≤x＜80，80≤x＜90，90≤x≤100）
b．乙部门成绩如下：
40 52 70 70 71 73 77 78 80 81
82 82 82 82 83 83 83 86 91 94
c．甲、乙两部门成绩的平均数、方差、中位数如下：
平均数 | 方差 | 中位数 | |
甲 | 79.6 | 36.84 | 78.5 |
乙 | 77 | 147.2 | m |
d．近五年该单位参赛员工进入复赛的出线成绩如下：
2014年 | 2015年 | 2016年 | 2017年 | 2018年 | |
出线成绩（百分制） | 79 | 81 | 80 | 81 | 82 |
根据以上信息，回答下列问题：
（1）写出表中m的值；
（2）可以推断出选择 部门参赛更好，理由为 ；
（3）预估（2）中部门今年参赛进入复赛的人数为 ．
