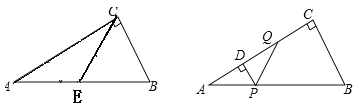��Ŀ����
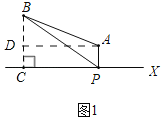
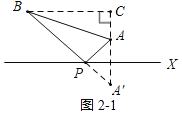
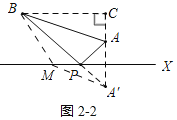
����Ŀ�������Ķ�ʩ��Ͽ�ȣ�A�������缶��Ȼ�������Ƕ�ɽ��B��λ�ڱ�ֱ�Ļ�����ٹ�·Xͬ�࣬AB��50km��A��B��ֱ��X�ľ���ֱ�Ϊ10km��40km��Ҫ�ڻ�����ٹ�·����һ������P����A��B�����������οͣ�С����������ַ�����ͼ1�Ƿ���һ��ʾ��ͼ��AP��ֱ��X��ֱ������ΪP����P��A��B�ľ���֮��S1��PA+PB��ͼ2�Ƿ�������ʾ��ͼ����A����ֱ��X�ĶԳƵ���A'������BA����ֱ��X�ڵ�P����P��A��B�ľ���֮��S2��PA+PB

��1��S1��_____km��S2��_____km��
��2��PA+PB����СֵΪ_____km��
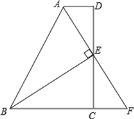
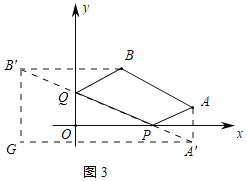
��3���⽨�Ķ�ʩ���żҽ���ٹ�·�뻦����ٹ�·��ֱ��������ͼ3��ʾ��ֱ������ϵ��B��ֱ�ߵľ�Ϊ30km��������X�Ժ�P�Ը���һ������P��Q��ʹP��A��B��Q��ɵ��ı��ε��ܳ���С�����ó�����P�͵�Q��λ�ã������СֵΪ_____km��
���𰸡���40![]() +10��
+10�� ![]()
![]() ��50+50
��50+50![]() ����
����
��������
��1�����ݹ��ɶ����ֱ����S1��S2��ֵ���ɣ�
��2���ڹ�·������һ��M������MA��MB��MA'������Գ�֪MA��MA���������ε����߹�ϵ�ó�MB+MA��MB+MA'��A'B���ó�S2��BA'Ϊ��С��
��3����A������x��ĶԳƵ�A'����B������y��ĶԳƵ�B'������A'B'����x���ڵ�P����y���ڵ�Q�����A'B'��ֵ���ɣ��ڹ�·������һ��M������MA��MB��MA'������Գ�֪MA��MA�������������߹�ϵ�ó�MB+MA��MB+MA'��A'B��S2��BA'Ϊ��С�����ɵó��𰸣�
�⣺��1����ͼ1�У���B��BC��X��C��AD��BC��D����CP��AD��
��BC��40km��
�֡�AP��10��
��BD��BC��CD��40��10��30km��
����ABD��AD��![]() ��40��km����
��40��km����
��CP��40km��
��Rt��PBC��BP��![]() ��
��![]() ��40
��40![]() ��km����
��km����
��S1��40![]() +10��km����
+10��km����
��ͼ2��1�У���B��BC��AA������ΪC��
��A��C��50km��
�֡�BC��40km��
��BA'��![]() ��10
��10![]() ��km����
��km����
����Գ�֪��PA��PA'��
��S2��BA'��10![]() km��
km��
�ʴ�Ϊ����40![]() +10����10
+10����10![]() ��
��
����Գ�֪MA��MA'��
��MB+MA��MB+MA'��A'B��
��S2��BA'��10![]() kmΪ��С��
kmΪ��С��
��PA+PB����СֵΪ10![]() km��
km��
�ʴ�Ϊ��10![]() ��
��
��3����A������x��ĶԳƵ�A'����B����y��ĶԳƵ�B'������A'B'����x���ڵ�P����y���ڵ�Q����ͼ3��ʾ��
��P��Q������
��A'��B'�ֱ���x�ᡢy���ƽ���߽��ڵ�G��
B��G��40+10��50km��A��G��30+30+40��100km��
A'B'��![]() ��50
��50![]() ��km����
��km����
��AB+AP+BQ+QP��AB+A��P+PQ+B��Q��50+50![]() km��
km��
�������ı��ε��ܳ�Ϊ��50+50![]() ��km��
��km��
�ʴ�Ϊ����50+50![]() ����
����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��ij�̵�����ι���![]() ������Ʒ�������ۣ����ι���ͬһ����Ʒ�Ľ�����ͬ������������±���ʾ��
������Ʒ�������ۣ����ι���ͬһ����Ʒ�Ľ�����ͬ������������±���ʾ��
��������(��) | �����������(Ԫ) | ||
|
| ||
��һ�� | 30 | 40 | 3800 |
�ڶ��� | 40 | 30 | 3200 |
(1) ��![]() ������Ʒÿ���Ľ��۷ֱ��Ƕ���Ԫ��
������Ʒÿ���Ľ��۷ֱ��Ƕ���Ԫ��
(2) �̳�����![]() ����Ʒ��ÿ��30Ԫ���ۣ�
����Ʒ��ÿ��30Ԫ���ۣ�![]() ����Ʒ��ÿ��100Ԫ���ۣ�Ϊ�����г������蹺��
����Ʒ��ÿ��100Ԫ���ۣ�Ϊ�����г������蹺��![]() ������Ʒ��1000������
������Ʒ��1000������![]() ����Ʒ������������
����Ʒ������������![]() ����Ʒ������4������������������Ľ�����������ȷ���������
����Ʒ������4������������������Ľ�����������ȷ���������