题目内容
【题目】如图,在平面直角坐标系中,点A的坐标为(2,3)且AO=BO,∠AOB=90°则点B的坐标为( )

A.(2,3)B.(-3,2)C.(-3,-2)D.(-2,3)
【答案】B
【解析】
过A作AC⊥x轴,垂足为C,作BD⊥x轴垂足为D.证明△AOC和△BOD全等,那么B的横坐标就是OD长的相反数,B的纵坐标就是OC长的绝对值,由此可得出B的坐标.
解:作AC⊥x轴,垂足为C,作BD⊥x轴垂足为D.

则∠ACO=∠ODB=90°,
∴∠AOC+∠OAC=90°.
又∵∠AOB=90°,
∴∠AOC+∠BOD=90°
∴∠OAC=∠BOD.
在△ACO和△ODB中
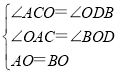
∴△ACO≌△ODB(AAS).
∴OD=AC=3,DB=OC=2.
∴点B的坐标为(-3,2).
故选B.

练习册系列答案
相关题目