题目内容
【题目】如图，在△ABF中，BE⊥AF垂足为E，AD∥BC，且AF平分∠DAB，求证：（1）FC=AD；（2）AB=BC+AD．
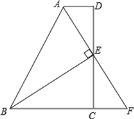
【答案】（1）详见解析；（2）详见解析.
【解析】
（1）根据平行线性质得到∠DAF=∠F，根据角平分线定义得到∠BAF=∠DAF，进而得到∠F=∠BAF，根据等角对等边得到AB=BF，根据等腰三角形三线合一得到AE=EF，利用ASA证得ADE≌△FCE，即可得证；
（2）由（1）中三角形全等可知AB=BF，AD=FC，利用等量代换即可解决问题.
（1）证明：∵AD∥BC
∴∠DAF=∠F
∵AF平分∠DAB
∴∠BAF=∠DAF
∴∠F=∠BAF
∴AB=BF
又 ∵BE⊥AF
∴AE=EF
在△ADE和△FCE中
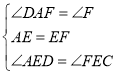
∴△ADE≌△FCE(ASA）
∴FC=AD
（2）证明：∵AB=BF AD=FC
又∵BF=BC+CF
∴AB=BC+AD
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
