题目内容
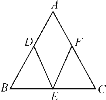
【题目】如图,在Rt△ABC中,∠C=90°,∠A=30°,取斜边AB的中点E,易得△BCE是等边三角形,从而得到“直角三角形中,30°角所对的直角边等于斜边的一半”利用这个结论解决问题:
如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=4,若动点P从点A出发,沿AB以每秒2个单位长度的速度向终点B运动.过点P作PD⊥AC于点D(点P不与点A.B重合),作∠DPQ=60°,边PQ交射线DC于点Q.设点P的运动时间为t秒.
(1)用含t的代数式表示线段DC的长;
(2)当线段PQ的垂直平分线经过△ABC一边中点时,直接写出t的值.
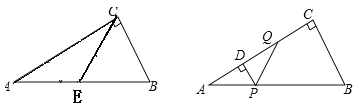
【答案】(1)![]() ;(2)t的值为
;(2)t的值为![]() 或
或![]() 或
或![]()
【解析】
(1)在Rt△ABC中,利用结论可得![]() ,可由勾股定理求出AC,在Rt△ADP中,由题意AP=2t,PD=t,用勾股定理可表示出AD,再用DC=AC-AD即可;
,可由勾股定理求出AC,在Rt△ADP中,由题意AP=2t,PD=t,用勾股定理可表示出AD,再用DC=AC-AD即可;
(2)分三种情况讨论,①当PQ的垂直平分线与PQ交于点G,且经过AB的中点F时,易证△PAD≌QPD,△PFG≌PAD,可得PF=AP=2t,而F为AB的中点,利用AP+PF=![]() AB可求t;
AB可求t;
②当PQ的垂直平分线经过AC的中点M时,可在Rt△MGQ中,求出MQ,然后利用AM+MQ=2AD可求出t;
③当PQ的垂直平分线经过BC的中点N,与AB的延长线交于H点时,
易证△PHG≌△PAD,则PH=AP=2t,然后利用等角对等边得到BH=BN=1,再由AH=AB+BN可求出t.
(1)在Rt△ABC中,利用结论可得![]() ,
,
∴![]()
在Rt△ADP中,由题意AP=2t,PD=t,
∴![]() ,
,
∴![]()
∵点P不与点A.B重合,∴![]()
故![]() .
.
(2)①当PQ的垂直平分线与PQ交于点G,且经过AB的中点F时,如图1,

在△APD和△QPD中,

∴![]()
∴PA=PQ,∠PQD=∠A=30°,AD=QD=![]()
∵GF是PQ的中垂线,∴![]() ,
,
在△APD和△FPG中,

∴![]()
∴PA=PF=2t
∵F为AB中点,∴AF=PA+PF=![]() AB,
AB,
即2t+2t=2,解得t=![]()
②当PQ的垂直平分线经过AC的中点M时,如图2,

由①可知PG=QG=![]() PQ=t,
PQ=t,
在Rt△MGQ中,设MG=x,∵∠MQG=30°,∴MQ=2x
由勾股定理得![]()
即![]() ,解得
,解得![]() 或
或![]() (舍去)
(舍去)
∴![]() ,
,
∵M为AC的中点,∴AM=![]() AC=
AC=![]() ,
,
AM+MQ=2AD,即![]() +
+![]() =
=![]() ,解得t=
,解得t=![]()
③当PQ的垂直平分线经过BC的中点N,与AB的延长线交于H点时,如图3,

在Rt△PFG中,![]() ,
,
∵∠ABC=∠H+∠BNH=60°,∴∠BNH=∠H=30°,∴BH=BN=![]() =1
=1
同①可证△PHG≌△PAD,∴PH=PA=2t,
由AB+BH=PA+PH=2PA得4+1=4t,解得t=![]()
综上,当线段PQ的垂直平分线经过△ABC一边中点时,t的值为![]() 或
或![]() 或
或![]() .
.