题目内容
【题目】完成下列推理过程
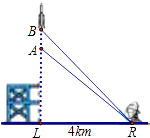
已知：∠C+∠CBD=180°，∠ABD=85°，∠2=60°，求∠A的度数.
解：∵∠C+∠CBD=180°（已知）
∴DB∥CE（ ）
∴∠1＝ ( )
∵∠2＝∠3（ ）
∴∠1＝∠2=60° ( )
又∵ ∠ABD=85°（已知）
∴∠A＝180°-∠ABD-∠1= （三角形三内角和为180°）
【答案】同旁内角互补，两直线平行；∠3；两直线平行，同位角相等；对顶角相等；等量代换；35°．
【解析】
根据平行线的判定定理和性质定理、三角形内角和定理填空即可．
解：∵∠C+∠CBD=180°（已知）
∴DB∥CE（同旁内角互补，两直线平行）
∴∠1＝∠3（两直线平行，同位角相等）
∵∠2＝∠3（对顶角相等）
∴∠1＝∠2=60°（等量代换）
又∵ ∠ABD=85°（已知）
∴∠A＝180°-∠ABD-∠1=35°（三角形三内角和为180°）
故答案为：同旁内角互补，两直线平行；∠3；两直线平行，同位角相等；对顶角相等；等量代换；35°．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
