Question

【题目】如图，一枚运载火箭从地面L处发射，当火箭到达A点时，从位于距发射架底部4km处的地面雷达站R（LR=4）测得火箭底部的仰角为43°．1s后，火箭到达B点，此时测得火箭底部的仰角为45.72°．这枚火箭从A到B的平均速度是多少 （结果取小数点后两位）？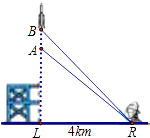

（参考数据：sin43°≈0.682，cos43°≈0.731，tan43°≈0.933，
sin45.72°≈0.716，cos45.72°≈0.698，tan45.72°≈1.025）

Answer 1

【答案】解：∵在Rt△ALR中，tan43°= ，LR=4，

∴AL=4×0.933=3.732，

∵在Rt△BLR中，tan45.72°= ，LR=4，

∴BL=4×1.025=4.1，

∴AB=4.1﹣3.732=0.368≈0.37，

∵火箭从A到B用时1s，

∴火箭从A到B的平均速度为：0.37÷1=0.37km/s，

即这枚火箭从A到B的平均速度是0.37km/s．

【解析】根据直角三角形的三角函数值在Rt△ALR中，tan43°的值，求出AL的值，由在Rt△BLR中，tan45.72°的值，求出BL的值，得到AB的值，由火箭从A到B用时1s，得到火箭从A到B的平均速度.
【考点精析】通过灵活运用关于仰角俯角问题，掌握仰角：视线在水平线上方的角；俯角：视线在水平线下方的角即可以解答此题．