题目内容
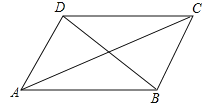
【题目】如图,在四边形ABCD中,AD∥BC,∠BAD=90°,对角线BD⊥DC.
(1)求证:△ABD∽△DCB;
(2)如果AD=4,BC=9,求BD的长.
【答案】
(1)证明:△ABD与△DCB相似,理由如下:
∵AD∥BC,
∴∠ADB=∠DBC.
∵BD⊥DC,
∴∠BDC=90°.
∵∠BAD=90°,
∴∠BAD=∠BDC.
∴△ABD∽△DCB.
(2)解:∵△ABD∽△DCB,
∴ ![]() .
.
∴BD2=ADCB.
∵AD=4,BC=9,
∴BD=6.
【解析】(1)根据平行线的性质两直线平行内错角相等,再根据两角对应相等两三角形相似;(2)根据相似三角形的性质得到比例,求出BD的长.
【考点精析】本题主要考查了相似三角形的判定与性质的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
【题目】某超市第一次用6000元购进甲、乙两种商品,其中甲商品件数的2倍比乙商品件数的3倍多20件,甲、乙两种商品的进价和售价如下表(利润=售价﹣进价):
甲 | 乙 | |
进价(元/件) | 20 | 28 |
售价(元/件) | 26 | 40 |
(1)该超市第一次购进甲、乙两种商品的件数分别是多少?
(2)该超市将第一次购进的甲、乙两种商品全部卖出后一共可获得多少利润?
(3)该超市第二次以同样的进价又购进甲、乙两种商品.其中甲商品件数是第一次的2倍,乙商品的件数不变.甲商品按原价销售,乙商品打折销售.第二次甲、乙两种商品销售完以后获得的利润比第一次获得的利润多560元,则第二次乙商品是按原价打几折销售的?