��Ŀ����
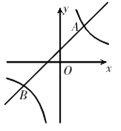
����Ŀ����ͼ1��2��3�ֱ��ʾ�ס��ҡ���������A�ص�B�ص�·��ͼ����֪
��·��Ϊ��A��C��B��
�ҵ�·��Ϊ��A��D��E��F��B������EΪAB���е㣻
����·��Ϊ��A��I��J��K��B������J��AB�ϣ���AJ��JB��

������[��]��ʾ[ֱ��ǰ��]�������ͼ1��ͼ2��ͼ3�����ݣ��ж������н�·�߳��ȵĴ�С��ϵΪ��������
A. ��=��=�� B. �ף��ң��� C. �ң������� D. �����ң���
���𰸡�A
���������������ɽǵĶ�������֪��2��3�е����������εĶ�Ӧ�߶���ƽ�е�������ͼ2��ͼ3�е������ζ���ͼ1�е����������ƣ�����ͼ2������ȫ����ͼ3������������
������������Ϸ���������ͼ2�ɵ�AE=BE��AD=EF��DE=BE��
��AE=BE=![]() AB����AD=EF=
AB����AD=EF=![]() AC��DE=BE=
AC��DE=BE=![]() BC�����=����
BC�����=����
ͼ3��ͼ1������������������������ ![]() =
=![]() =
=![]() =
=![]() =
=![]() ��
��
��AJ+BJ=AB����AI+JK=AC��IJ+BK=BC��
���=�������=��=����
��ѡA��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��ijʯ����ϩ��ij���������ס����������ϵ������Ϣ���±����������������⣺
������ | �ɱ��� | ���۴����� | |
�������� | 2100��Ԫ/�֣� | 800��Ԫ/�֣� | 200��Ԫ/�֣� |
�������� | 2400��Ԫ/�֣� | 1100��Ԫ/�֣� | 100��Ԫ/�֣� ��ÿ�»���֧���豸������ά����20000Ԫ |
��1����ó���ÿ�������ס����������ϸ�x�֣�����ֱ�Ϊy1Ԫ��y2Ԫ���ֱ����y1��y2��x�ĺ�����ϵʽ(ע������=������-��֧��)��
��2����֪�ó���ÿ�������ס����������Ͼ�������400�֣���ij��Ҫ�����ס����������Ϲ�700�֣�����������ס������ϸ����ٶ�ʱ����õ������������������Ƕ��٣�