��Ŀ����
����Ŀ��Ϊ�����ҹ�����ά�Ͳ��ӹٱ����������ͨ��A�ۿڡ�B�ۿڷֱ�����100�ֺ�50���������ʣ���֪�������ڼײֿ����80�֣��Ҳֿ����70�֣����Ӽס������ֿ��������ʵ��ۿ�A�ķ��÷ֱ�Ϊ14Ԫ/�֣�20Ԫ/�֣��Ӽס������ֿ��������ʵ��ۿ�B�ķ��÷ֱ�Ϊ10Ԫ/�֡�8Ԫ/�֣�
������Ӽײֿ�����A�ۿ�x�֣�����д����
��һ
�ۿ� | �Ӽײֿ��ˣ��֣� | ���Ҳֿ��ˣ��֣� |
A�� | �� �� | �� �� |
B�� | �� �� | �� �� |
����
�ۿ� | �Ӽײֿ��˵��ۿڷ��ã�Ԫ�� | ���Ҳֿ��˵��ۿڷ��ã�Ԫ�� |
A�� | 14x | �� �� |
B�� | �� �� | �� �� |
����������ɴ˴�������������ʡ���õĵ��䷽������˵�����ɣ�
���𰸡�����x��100��x��80��x��x��30��20��100��x����10��80��x����8��x��30�������Ѽײֿ��ȫ������A�ۿڣ��ٴ��Ҳֿ���20����A�ۿڣ��Ҳֿ�����µ�ȫ������B�ۿڣ����ɼ�����
��������
���������������ʾ���ײֿ���Ҳֿ�ֱ�����A��B���ۿڵ������������ɵ�����ϵ�����˷�=�ײֿ�����A�ۿڵķ���+�ײֿ�����B�ۿڵķ���+�Ҳֿ�����A�ۿڵķ���+�Ҳֿ�����B�ۿڵķ�����ʽ�����������ݲ���ʽ��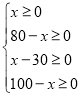 �ó�x��ȡֵ��
�ó�x��ȡֵ��
��������Ϊ���õĺ���Ϊһ�κ������������Կ�֪��y��x��������٣���x=80ʱ��y��С���������Сֵ��д�����䷽����
������Ӽײֿ���x����A�ۿڣ���Ӽײֿ�����B�ۿڵ��У�80��x���֣����Ҳֿ�����A�ۿڵ��У�100��x���֣�����B�ۿڵ���50����80��x��=��x��30���֣�
���÷ֱ�Ϊ14xԪ��10��80��x��Ԫ��20��100��x��Ԫ��8��x��30��Ԫ��
�ʴ𰸷ֱ�Ϊx��100��x��80��x��x��30��20��100��x����10��80��x����8��x��30����
������Ϊy=14x+20��100��x��+10��80��x��+8��x��30��=��8x+2560��
�������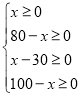 ��
��
��x��ȡֵ��Χ��30��x��80��
��Ϊy��x��������٣����Ե�x=80ʱ���˷���С��
��x=80ʱ��y=��8��80+2560=1920��
��ʱ����Ϊ���Ѽײֿ��ȫ������A�ۿڣ��ٴ��Ҳֿ���20����A�ۿڣ��Ҳֿ�����µ�ȫ������B�ۿڣ�

 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�