题目内容
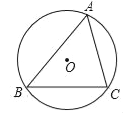
【题目】如图，△ABC内接于⊙O．
（1）作∠B的平分线与⊙O交于点D（用尺规作图，不用写作法，但要保留作图痕迹）；
（2）在（1）中，连接AD，若∠BAC=60°，∠C=66°，求∠DAC的大小．
【答案】（1）答案见解析；（2）27°．
【解析】试题分析：（1）根据角平分线的尺规作图即可得；
（2）根据三角形的内角和得出∠ABC=180°-∠BAC-∠C=54°，由作图可知BD平分∠ABC，从而得出∠DAC=∠DBC=
∠ABC=27°．
试题解析：（1）如图所示，BD即为所求．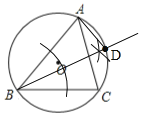
（2）∵∠BAC=60°、∠C=66°，
∴∠ABC=180°-∠BAC-∠C=54°，
由作图可知BD平分∠ABC，
∴∠DAC=∠DBC=
∠ABC=27°．
练习册系列答案
相关题目
【题目】受气候的影响，某超市蔬菜供应紧张，需每天从外地调运蔬菜1000斤．超市决定从甲、乙两大型蔬菜棚调运蔬菜，已知甲蔬菜棚每天最多可调出800斤，乙蔬菜棚每天最多可调运600斤，从两蔬菜棚调运蔬菜到超市的路程和运费如下表：
到超市的路程（千米） | 运费（元/斤·千米） | |
甲蔬菜棚 | 120 | 0.03 |
乙蔬菜棚 | 80 | 0.05 |
（1）若某天调运蔬菜的总运费为3840元，则从甲、乙两蔬菜棚各调运了多少斤蔬菜？
（2）设从甲蔬菜棚调运蔬菜
斤，总运费为
元，试写出与的函数关系式，怎样安排调运方案才能使每天的总运费最省？
