题目内容
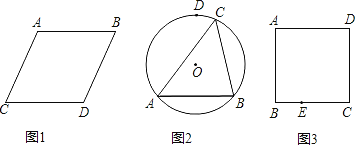
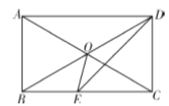
【题目】如图，已知矩形
中，
与
相交于
，
平分
交
于
，
，则
的度数为_______．
【答案】
【解析】
先求出∠ADB，再说明三角形ODC是等边三角形，推出CD=OC，CE=CD，求出CE=OC，求出∠COE=∠OEC和∠OCB=30°即可解答．
解：∵四边形ABCD是矩形，
∴AD//BC，∠ADC=90°，OA=OC，OB=OD，AC=BD，
∵DE平分∠ADC，
∴∠ADE=∠CDE=
∠ADC=45°，
∵∠BDE=15°，
∴∠ADB=∠ADE-∠BDE=30°，
∵AD∥BC，
∴∠ADB=∠DBC=30°，
∴OA=OD=OB=OC，
∴∠OBC=∠OCB=30°，
∴∠DOC=∠OBC+∠OCB=60°，
∵OD=OC，
∴△ODC是等边三角形，
∴DC=OC，
∵AD∥BC，
∴∠ADE=∠DEC
∴∠ADE=∠CDE，
∴∠DEC=∠CDE，
∴CE=DC
∴CE=OC，
∴∠COE=∠OEC，
∵∠OCB=30°，
∴∠COE=（180°-∠OCE）=75°．
故答案为75°．
练习册系列答案
相关题目
【题目】为保障我国海外维和部队官兵的生活，现需通过A港口、B港口分别运送100吨和50吨生活物资．已知该物资在甲仓库存有80吨，乙仓库存有70吨，若从甲、乙两仓库运送物资到港口A的费用分别为14元/吨，20元/吨；从甲、乙两仓库运送物资到港口B的费用分别为10元/吨、8元/吨．
（Ⅰ）设从甲仓库运往A港口x吨，试填写表格．
表一
港口 | 从甲仓库运（吨） | 从乙仓库运（吨） |
A港 |
|
|
B港 |
|
|
表二
港口 | 从甲仓库运到港口费用（元） | 从乙仓库运到港口费用（元） |
A港 | 14x |
|
B港 |
|
|
（Ⅱ）给出能完成此次运输任务的最节省费用的调配方案，并说明理由．
