Question

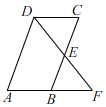
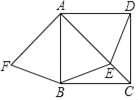
【题目】如图，正方形ABCD，动点E在AC上，AF⊥AC，垂足为A，AF＝AE．

（1）BF和DE有怎样的数量关系？请证明你的结论；

（2）在其他条件都保持不变的是情况下，当点E运动到AC中点时，四边形AFBE是什么特殊四边形？请证明你的结论．

Answer 1

【答案】（1）BF＝DE；（2）正方形

【解析】

（1）由正方形的性质可得AB＝AD，∠DAC＝∠BAC＝45°，通过证明△AFB≌△AED，可得BF＝DE；

（2）由正方形的性质可得AE＝BE，∠AEB＝90°，通过证明△ABF≌△ABE，可得BF＝BE，可证四边形AFBE是菱形，且AF⊥AE，可证四边形AFBE是正方形．

证明：（1）BF＝DE，

理由如下：∵四边形ABCD是正方形，

∴AB＝AD，∠DAC＝∠BAC＝45°，

∵AF⊥AC，

∴∠FAB＝∠BAC＝∠DAC＝45°，且AD＝AB，AF＝AE，

∴△AFB≌△AED（SAS），

∴BF＝DE，

（2）正方形，

理由如下：∵四边形ABCD是正方形，点E是AC中点，

∴AE＝BE，∠AEB＝90°

∵∠FAB＝∠BAC＝45°，且AB＝AB，AF＝AE，

∴△ABF≌△ABE（SAS），

∴BF＝BE，

∴AE＝BE＝BF＝AF，

∴四边形AFBE是菱形，且AF⊥AE，

∴四边形AFBE是正方形