题目内容
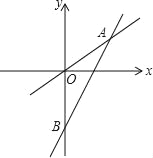
【题目】C点的坐标为（4，4），A为y轴负半轴上一动点，连CA，CB⊥CA交x轴于B．
（1）求OB﹣OA的值；
（2）E在x轴正半轴上，D在y轴负半轴上，∠DCE＝45°，转动∠DCE，求线段BE、DE和AD之间的数量关系．
【答案】（1）8；（2）①当D在OA的延长线上时，DE＝AD+BE；②当D在边OA上时，DE＝BE﹣AD
【解析】
（1）如图1，作辅助线，证明△CQA≌△CPB（AAS），可得PB=AQ，根据线段的和与差可得结论；
（2）存在两种情况：
①当D在OA的延长线上时，如图2，作辅助线，证明△CAD≌△CBM（ASA）和△DCE≌△MCE（SAS），得DE=EM，AD=BM，相加可得结论．
②当D在边OA上时，如图3，同理可得；DE=BE-AD．
解：（1）如图1，过C作CQ⊥y轴于Q，过C作CP⊥OB于P，
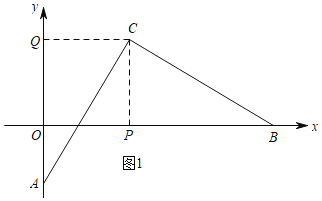
∵C（4，4），
∴CQ＝CP＝OQ＝OP＝4，
∵AC⊥BC，
∴∠ACB＝∠ACP+∠BCP＝∠BCP+∠PBC＝90°，
∴∠ACP＝∠PBC，
∵OA∥PC，
∴∠CAQ＝∠ACP＝∠PBC，
∵∠CPB＝∠CQA＝90°，
∴△CQA≌△CPB（AAS），
∴PB＝AQ，
∴OB﹣OA＝OP+PB﹣OA＝OP+AQ﹣OA＝OP+OQ＝8；
（2）分两种情况：
①当D在OA的延长线上时，DE＝AD+BE，理由是：
如图2，过C作CM⊥CD，交x轴于M，
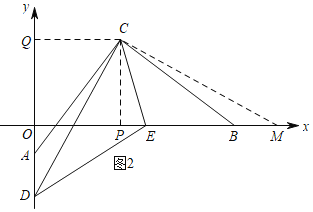
∵AC⊥BC，
∴∠ACD＝∠BCM，
由（1）知：△CQA≌△CPB，
∴AC＝BC，∠CAQ＝∠PBC，
∴∠DAC＝∠MBC，
∴△CAD≌△CBM（ASA），
∴BM＝AD，CD＝CM，
∵∠ACB＝90°，∠DCE＝45°，
∴∠ACD+∠BCE＝45°＝∠BCM+∠BCE＝∠ECM，
∵CE＝CE，
∴△DCE≌△MCE（SAS），
∴DE＝EM，
∴EM＝BE+BM＝BE+AD＝DE，
即DE＝AD+BE．
②当D在边OA上时，DE＝BE﹣AD，理由是：
如图3，过C作CM⊥CD，交x轴于M，
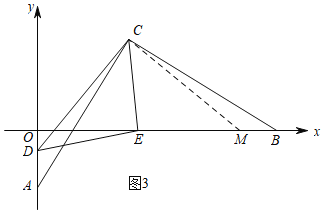
同理得△CAD≌△CBM（ASA），
∴BM＝AD，CD＝CM，
同理得：△DCE≌△MCE（SAS），
∴DE＝EM，
∴EM＝BE﹣BM＝BE﹣AD＝DE，
即DE＝BE﹣AD．
